AcWing-1326.军训队列

¶首先来首歌曲来放松一下吧！

题目链接：1326. 军训队列

¶题目背景：

¶题目描述

有 n 名学生参加军训，军训的一大重要内容就是走队列，而一个队列的不整齐程度是该队中最高的学生的身高与最矮的学生的身高差值的平方。

现在要将 n 名参加军训的学生分成 k 个队列，每个队列的人数可以是任意非负整数。

在安排队列时希望所有队列的不整齐度之和尽量小，请问不整齐度之和最小可以是多少？

¶输入格式

第一行两个整数 n,k，表示学生人数和队列数。

第二行 n 个整数，依次表示每名学生的身高。

¶输出格式

一个整数表示答案。

¶数据范围

对于10%的数据，k=1；
对于另外10%的数据，k=2；
对于另外10%的数据，k=3；
对于另外10%的数据，k=4；
对于另外10%的数据，1≤n,k≤5；
对于另外10%的数据，1≤n,k≤10；
对于另外20%的数据，1≤n,k≤100；
对于另外5%的数据，n=k=500;
对于所有的数据，1≤n,k≤500，0≤ 学生身高 ≤200

¶输入样例：

1 2	`3 2 170 180 168`

¶输出样例：

¶题目分析：

这对我来说是一道难题，用到了贪心和动态规划：

我也是第一次接触Dp。

我的理解动态规划就是从小集合算到大集合，找大的集合和小的集合的关系，即可实现后面用到的前面已经算出来的效果！

尽我的能力写了一篇足够详细的题解：

¶题目要求：

n 个人，分成 k 组，求 k 组的最大最小值差的平方的最小值，也就是在所有分法中找一个最优解！

¶解题思路：

贪心 + Dp

首先，分成 k 组，一定要让 k 组不空，因为如果分成k - 1组，和从k - 1组里拿出一个人给了第k 组，后者得到的结果一定不会比前者更坏，最优解一定不会变大，也就是说，全部分成k组得到的结果会更优，自己好好想想！
用二维数组 f[i][j] 表示将前 i 个人分成 j 组！

前提：当然是从小到大排好序了！

探讨 f[i][j] 的情况：

将 i 个人划分为 j 组，考虑一下最后一组的情况，也就是要保证最后一组之前要有j - 1组，每组至少一个人，所以最后一组的起始点最小值也得是 j , 而总共i 个人，那么最后一组的起始值的范围是 j <= k <= i ，也就是f[i][j] 的划分集合共有i - j 种，而最优解一定为其中一种，如下图：

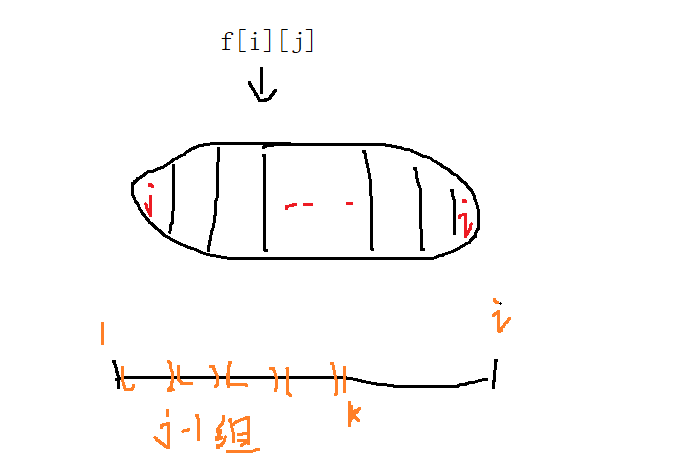
继续看图：最终f[i][j] 的值当然就是前面的 j - 1 组的结果加上最后一组的和了：

前面j - 1 组，相当于从 k - 1 个人中划分 j - 1组，即f[k - 1][j - 1] :

所以：最终结果：

f[i][j] = min(f[i][j], f[k - 1][j - 1] + (a[i] - a[k]) * (a[i] - a[k]));

计算最小值，当然要将f数组初始化为较大值：0x3f 。

划分组数 j 要保证不大于人数 i，不大于划分数 m 。

边界：当然是f[1][1] , 要想的到该值，当然需要有 f[0][0] 。将0个人划分为 0 组，结果当然为0；处理好边界值：f[0][0] = 0;

k 的取值范围正如上面所讲，j 到 i 。

最后输出f[n][m] 即可！

¶官方题解视频：

yxc大神官方讲解

¶题解：

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

int n, m;
int a[510];
int f[510][510];

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> a[i];
	
	if(m >= n) 
	{
		cout << 0 << endl;
		return 0;
	}
	
	sort(a + 1, a + n + 1);
	memset(f, 0x3f, sizeof f);
	f[0][0] = 0;
	for(int i = 1; i <= n; i++)
	{
		for(int j = 1; j <= i && j <= m; j++)
		{
			for(int k = j; k <= i; k++)
			{
				f[i][j] = min(f[i][j], f[k - 1][j - 1] + (a[i] - a[k]) * (a[i] - a[k]));
			}
		}
	}
	cout << f[n][m] << endl;
	return 0;
}