首先来首歌曲来放松一下吧！

题目链接：112. 雷达设备

题目背景：

同样是贪心问题！

题目描述

假设海岸是一条无限长的直线，陆地位于海岸的一侧，海洋位于另外一侧。

每个小岛都位于海洋一侧的某个点上。

雷达装置均位于海岸线上，且雷达的监测范围为d，当小岛与某雷达的距离不超过d时，该小岛可以被雷达覆盖。

我们使用笛卡尔坐标系，定义海岸线为x轴，海的一侧在x轴上方，陆地一侧在x轴下方。

现在给出每个小岛的具体坐标以及雷达的检测范围，请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目。

输入格式

第一行输入两个整数n和d，分别代表小岛数目和雷达检测范围。

接下来n行，每行输入两个整数，分别代表小岛的x，y轴坐标。

同一行数据之间用空格隔开。

输出格式

输出一个整数，代表所需的最小雷达数目，若没有解决方案则所需数目输出“-1”。

数据范围

1≤n≤1000

输入样例：

1
2
3
4
3 2
1 2
-3 1
2 1

输出样例：

1
2

题目分析：

题目要求：

简单来说，就是给一条数轴，在数轴上方有一些点（小岛），要在数轴上放置雷达，使得可以使每个点都被覆盖住！

求达到目的的最小雷达数目！

解题思路：

雷达有一个半径值，当然处于半径内则可以覆盖！

首先先考虑一个点（x，y）,要想使得数轴上的雷达可以探测到，必须处于半径范围内，左右可以拓展的距离最大就是以点（x，y）往出拉一条雷达的半径d，与数轴的交点就是可以拓展的最大距离，即只要在[a，b] 范围内就可以保证当前点处于雷达可探测范围！

如下图：

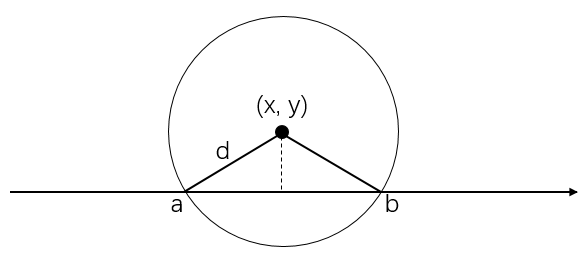
若发现无交点，即当前点太高，即使雷达放在正下方都够不着，超过了雷达的范围，则直接返回-1即可！

判断条件：y > d 时！够不着！

计算区间a，b值可以利用勾股定理即可！

这样我们可以得到每一个点的雷达取值区间，现在问题就从二维变为了一维的区间问题！

具体解法：

  • 我们可以给每个区间按照右端点从小到大排序！
  • 扫描每一个区间，看这个区间内是否有雷达？
    • 若没有雷达，则在当前区间右端点放置一颗雷达
    • 若有雷达，则跳过即可

具体解释一下：

排好序后，如果前面有一个雷达则去看一下雷达有没有在当前点的区间，要知道：只有在当前点的区间内才能够得着这个点！

为了尽可能的使放一个雷达可以最好，最大的服务后面的的点的区间，可以将每个雷达放到该点区间的右端点即可！

既可以保证当前点被覆盖，又可以保证距离下一个点最近，达到最优的效果！

最后的最少的雷达数就是区间上可以放置的雷达数，即进去if条件的次数！

证明可以看一下下方yxc大神的证明！

yxc视频讲解，点击这里！

题解：

下一个区间要想判断是否在雷达的左或右边，可以简单的用一个last指针来动态指向雷达的位置，若区间没有雷达，则将last置为当前区间的右端点，否则跳过即可！

注意：因为勾股定理需要开方，所以区间使用double来存储！

数轴是正无穷到负无穷级别的，所以将last初值赋为负无穷大！

具体参考代码理解！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <cmath>
#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;
const double INF = 1e10;

struct Node
{
    double l, r;
};

bool cmp(Node a, Node b)
{
    return a.r < b.r;
}

int n, d;
Node a[N];

int main()
{
    cin >> n >> d;
    for(int i = 0, x, y; i < n; i++)
    {
        cin >> x >> y;
        
        if(y > d)
        {
            cout << -1 << endl;
            return 0;
        }
        
        double l = x - sqrt(d * d - y * y), r = x + sqrt(d * d - y * y);
        a[i] = {l, r};
    }
    
    sort(a, a + n, cmp);
    
    int res = 0;
    double last = -INF;
    for(int i = 0; i < n; i++)
    {
        if(a[i].l > last)
        {
            res ++;
            last = a[i].r;
        }
    }
    
    cout << res << endl;
    return 0;
}