首先来首歌曲来放松一下吧！

题目链接：788. 逆序对的数量

题目背景：

题目描述

给定一个长度为n的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i < j 且 a[i] > a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

1≤n≤100000

输入样例：

1
2
6
2 3 4 5 6 1

输出样例：

1
5

题目分析：

题目要求：

题目要求求出逆序对的数目，所谓逆序对就是后面的数小于前面的数就是一组！

解题思路：

首先，应该想到逆序对不就是从小大大排序时，需要交换的两者吗？所以可以使用冒泡排序，在进行交换时就进行++记录。

但是：很明显冒泡排序复杂度太大，是O(N) 的，一定超时。

所以又想到归并排序，归并排序也有逆序对的交换，所以也可以进行记录。时间复杂度为O(NlogN)！

归并排序模板！点击这里！

稍微解释一下归并排序，先分后合的思想：

分：将原来的一条链一直从中间切开，直到切到当前只有一个元素，这时，它是有序的。

合：将当前两个有序序列排好序用中间变量存储起来，最后再将中间序列还给原序列。

直到序列全部有序！

本题就是要在归并排序的过程中，产生逆序对的时候，进行记录：

其中res 就是用来记录的，res = mid - i + 1; 关于这里，要详细解释一下：

1
2
3
4
5
6
7
8
9
while(i <= mid && j <= r)
{
	if(a[i] <= a[j]) temp[k++] = a[i++];
	else
	{
		res += mid - i + 1; 
		temp[k++] = a[j++];
	}
}

首先：相邻的这两个序列，对序列本身自己来说，它是内部有序的，假如左边的序列大于右边的序列，由于左右都是有序的，那么左边的序列从当前位置 i 到 mid 结束时，都是要大于右边当前值的，所以逆序对不是1，而是 res += mid - i + 1; ， 至于为什么要这样算，因为等到右边的较小值被存储了之后，左边当前值以后真的值就没有机会和右边的被存储值进行比较了！

如图：

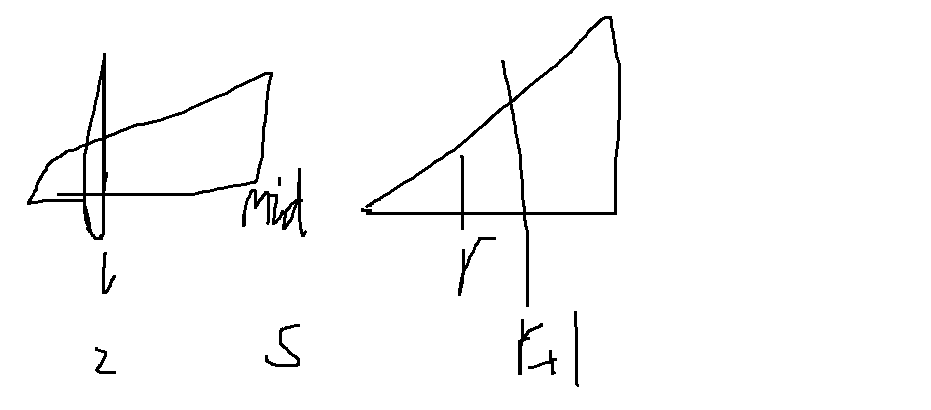
题解：

注意：最好使用long long 或许数据很大！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>

using namespace std;

const int N = 100050;
int a[N], temp[N];
long long n, res;

void merge_sort(int a[], int l, int r)
{
	if(l >= r) return;
	
	int mid = l + r >> 1;
	merge_sort(a, l, mid), merge_sort(a, mid + 1, r);
	
	int k = 0, i = l, j = mid + 1;
	while(i <= mid && j <= r)
	{
		if(a[i] <= a[j]) temp[k++] = a[i++];
		else
		{
			res += mid - i + 1; 
			temp[k++] = a[j++];
		}
	}
	while(i <= mid) temp[k++] = a[i++];
	while(j <= r) temp[k++] = a[j++];
	for(i = l, j = 0; i <= r; i++, j++) a[i] = temp[j];
}

int main()
{
	cin >> n;
	for(int i = 0; i < n; i++) cin >> a[i];
	merge_sort(a, 0, n - 1);
	cout << res << endl;
	return 0;
}