首先来首歌曲来放松一下吧！

题目链接：105. 七夕祭

此题为了理解折腾了一下午，写题解又写了一晚上！终于完整的记录了下来

题目背景：

本题运用了大量的数学公式化简，以及中位数性质等等，我会在题目分析当中进行详细介绍和解释！

题目描述

七夕节因牛郎织女的传说而被扣上了「情人节」的帽子。

于是TYVJ今年举办了一次线下七夕祭。

Vani同学今年成功邀请到了cl同学陪他来共度七夕，于是他们决定去TYVJ七夕祭游玩。

TYVJ七夕祭和11区的夏祭的形式很像。

矩形的祭典会场由N排M列共计N×M个摊点组成。

虽然摊点种类繁多，不过cl只对其中的一部分摊点感兴趣，比如章鱼烧、苹果糖、棉花糖、射的屋……什么的。

Vani预先联系了七夕祭的负责人zhq，希望能够通过恰当地布置会场，使得各行中cl感兴趣的摊点数一样多，并且各列中cl感兴趣的摊点数也一样多。

不过zhq告诉Vani，摊点已经随意布置完毕了，如果想满足cl的要求，唯一的调整方式就是交换两个相邻的摊点。

两个摊点相邻，当且仅当他们处在同一行或者同一列的相邻位置上。

由于zhq率领的TYVJ开发小组成功地扭曲了空间，每一行或每一列的第一个位置和最后一个位置也算作相邻。

现在Vani想知道他的两个要求最多能满足多少个。

在此前提下，至少需要交换多少次摊点。

输入格式

第一行包含三个整数N和M和T，T表示cl对多少个摊点感兴趣。

接下来T行，每行两个整数x, y，表示cl对处在第x行第y列的摊点感兴趣。

输出格式

首先输出一个字符串。

如果能满足Vani的全部两个要求，输出both；

如果通过调整只能使得各行中cl感兴趣的摊点数一样多，输出row；

如果只能使各列中cl感兴趣的摊点数一样多，输出column；

如果均不能满足，输出impossible。

如果输出的字符串不是impossible， 接下来输出最小交换次数，与字符串之间用一个空格隔开。

数据范围

1≤N,M≤100000
0≤T≤min(N∗M,100000)
1≤x≤N
1≤y≤M

输入样例：

1
2
3
4
5
2 3 4
1 3
2 1
2 2
2 3

输出样例：

1
row 1

题目分析：

题目要求：

就是 n 行 m 列的构成的 n * m 个交叉点，输入 t 个点的坐标，询问是否能使得每行的点数相同，每列的点数相同，若能相同，输出最小交换步数！

交换方法：上下左右交换，还有一个特殊的交换：每一行或每一列的第一个可以和每一行或每一列的最后一个交换，即可以看成环形的状态！

解题思路：

首先：想一个问题：什么情况才能让行或列所占点数相同？

很明显，行或列点数和只有是行或列的倍数时才可以。这样才可以平分，对吧！

答案前半部分很好判断，后半部分最小步数不太好判断！

接着：在想一个问题，在做行与行间点的交换时，即上下交换，会发现，上下交换是不会影响列的数目变化，毕竟上下交换，一定在那一列，那一列总和不会变！

同理：在做列与列的点的交换时，即左右交换，会发现，左右交换是不会影响行的数目变化，毕竟左右交换，一定在那一行，那一行总和不会变！

所以本题可以分为两个部分，一个行，一个列，分别取处理！毕竟不会互相影响！

这个题和均分纸牌问题类似：

读者可能已经想到了一个与此类似的经典问题“均分纸牌”。“均分.
纸牌”问题是说，有M个人排成一行，他们手中分别有C[1]~C[M]张纸牌，在每一
步操作中，可以让某个人把自己手中的一张纸牌交给他旁边的一个人，求至少需要多少步操作才能让每个人手中持有的纸牌数相等。

显然，“ 均分纸牌”问题当所有人手中持有的纸牌总数T能被M整除时有解。

我们这样想：假如可以均分，即最后牌数一样多时：

第一个人为了达到目标平均值 T/M ,要将多出来的 C[1] - T/M 给了第二个人，第二个人此时有 C[2] + C[1] - T/M张牌。

假如第一个人不够 T/M 张牌需要去第二个人处借 T/M - C[1]张牌，此时第二个人有C[2] + T/M - C[1]张牌。

终上：第一个人要想达到T/M张牌，必须去和下一个人借或给！结束之后第一个人变成了T/M张牌，发生的交换次数为|C[1] - T/M|次

第二个人当前的牌数为： C[2] + (C[1] - T/M)

为了达到T/M张牌，必须去和下一个人借或给！则要做 |C[2] + (C[1] - T/M) - T/M|次交换！

化简一下可以得到：第i个人需要交换次数为 |C[i] + C[i - 1] +…C[1] - i * T/M| 次交换！

最终交换次数就是将其求和即可！

会发现每一项都有一个前缀和：令G[i] 为C[i] 的前缀和，即最终次数变成了：

|G[i] - i* T/M| ：i 从 1到M求和即可！

注意：不用考虑某个人变为负数啥的，因为最终他都会去想后面的人来补齐！这就是拆东墙补西墙，但是不一样的是，这个最终会都补好！

继续：将每个人的初始牌数都减去T/M，得到相对于平均值的一些正负数，要想使得最终相等，那么每个人都得相对于平均值为0，即都是平均值才可以！

假设：令 A[i] = C[i] - T/M

此时第一个人需要交换次数为|A[1]|

第二个人为|A[2] + A[1]|

第i个人为|A[i] + A[i - 1] … + A[1]|

令S[i] 为A[i] 的前缀和，则：

第i个人交换次数为：|S[i]|

所以最终次数变为了：|S[i]| ，i从1到M求和！

到了这里，题目就简单多了！普通均分纸牌就结束了！

回归本题：这道题就是在均分纸牌的条件上，多了一个首和尾可以交换！成为了环形均分纸牌：

首先给出一个结论：

最优解下，一定存在两个人没有进行交换

如下图：

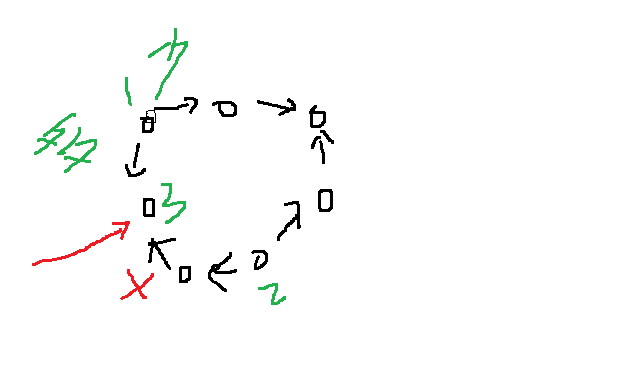
图：2号标错了，标在紧挨3号的位置才对。。。懒得换了！

假如发生了这样的交换，1号和2后都在给三号，我们要的是交换次数最少，最优！那么为什么不把2号到3号的直接砍断，让1号给三号多一点，给另一方少一点，这样不就可以减少交换次数吗？

没毛病，这样就反证了刚刚的结论！

现在我们只需要枚举在哪里有两个人没有发生交换即可！

假设发生在k处！

上面的那个求和公式则是在1号和M号之间断开了！即：|S[i]| ，i从1到M求和！

发生在K处的话，前缀和S[i]会发生什么变化：

如图：

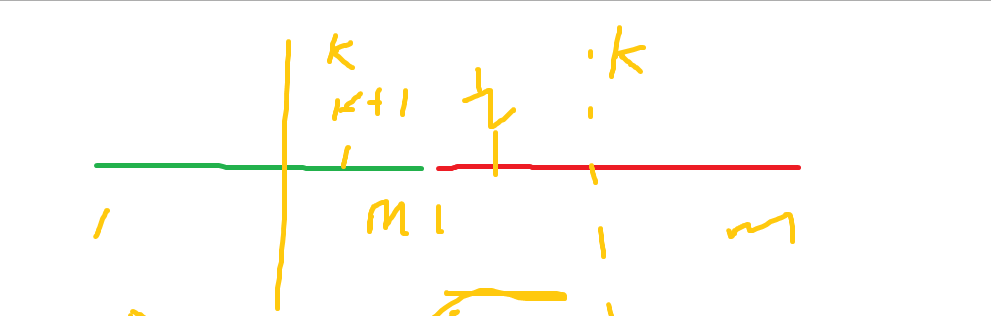
我们可以将1~M的长条进行多条拼接，即可得到在任意处砍断的完整长条，假设在K处砍断：前缀和发什么什么变化？

S[k + 1] -----------> S[k + 1] +( S[M] - S[k]) （可以在左边再延长一条线看出来）

S[k] ---------------> 0

S[1] ---------------> S[1] + (S[M] - S[k])

S[i] ---------------> S[i] + (S[M] - S[k])

然后又因为S[i] 是A[i] = C[i] - T/M 的前缀和，叨叨S[M]时，前面的都已经变为0了，即达到T/M了，最后一个人则自动达成最终的T/M，所以最后一项一定是0，不需要发生交换！

所以原式子：|S[i]| ，i从1到M求和！ 有了砍断部分的加入则变成了|S[i] - S[M]| - S[k]| 因为S[M]为0，则最终变为：|S[i] - S[k]|

最终交换次数为：|S[i] - S[k]| i从1到M求和

现在就是要找到砍断的地方，使得，这个式子求和和值最小！

看这个式子的几何意义：就是k到各个前缀和的距离，此时，没有什么点数，牌数，已经转变为了一个个前缀和，就像一个个条形的柱子，想统计学的柱形图一样，在中间找一个地方，使得到左右柱子的距离和最短！

眼熟吗？

这不就是刚刚做过的AcWing-104. 货仓选址 吗？

砍断处 k 相当于货仓位置，s[i] 相当于各个商店位置！

什么时候距离最小呢？

参考货仓选址的中位数证明！

所以只要将 砍断处选在 中位数的位置即可达到最优解！

本题解完毕！

可以看《算法竞赛进阶指南》的作者李煜东的讲解视频：大概在29分钟的时候！

题解：

注意：要用long long，数据很大！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <algorithm>

using namespace std;
typedef long long LL;

const int N = 1e5 + 10;
int n, m, t;
int a[N], b[N], f[N];

LL calc(int c[], int n)
{
    // c[i]-->A[i] = C[i] - T/M 
    // f[i]-->S[i] 为A[i]前缀和
    for(int i = 1; i <= n; i++) c[i] -= c[0]/n, f[i] = f[i - 1] + c[i]; 
    
    sort(f + 1, f + 1 + n);
    LL mid = f[n + 1 >> 1];
    
    LL res = 0;
    //求 |S[i] - S[k]| 的和
    for(int i = 1; i <= n; i++) res += abs(f[i] - mid);
    return res;
}

int main()
{
    cin >> n >> m >> t;
    for(int i = 1, x, y; i <= t; i++)
    {
        cin >> x >> y;
        a[x] ++, b[y] ++;
    }

    for(int i = 1; i <= n; i++) a[0] += a[i];
    for(int i = 1; i <= m; i++) b[0] += b[i];
    
    int row = a[0] % n, col = b[0] % m;
    if(!row && !col) cout << "both " << calc(a, n) + calc(b, m) << endl;
    else if(!row) cout << "row " << calc(a, n) << endl;
    else if(!col) cout << "column " << calc(b, m) << endl;
    else cout << "impossible";

    return 0;
}