首先来首歌曲来放松一下吧！

题目链接：104. 货仓选址

题目背景：

贪心，贪的我很服。。。

题目描述

在一条数轴上有 N 家商店，它们的坐标分别为 A1~AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式

第一行输入整数N。

第二行N个整数A1~AN。

输出格式

输出一个整数，表示距离之和的最小值。

数据范围

1≤N≤100000

输入样例：

1
2
4
6 2 9 1

输出样例：

1
12

题目分析：

题目要求：

有N个商店，要求放一个仓库使得到所有商店的距离和最小，输出最小值！

解题思路：

第一想法就是暴力扫描一遍，选出最小值即可！但是超时了，数据范围为1e5，平方就是1e10，肯定超时，详见题解一的代码：

正确思路：

先排序，使其变成一条链状的情况！

把a[0] ~ a[N-1]排序，设货仓在X坐标处，X左侧的商店有P家，右侧的商店有Q家。若P < Q，则每把仓库的选址向右移动1单位距离，距离之和就会变少Q - P.同理，若P > Q，则仓库的选址向左移动会使距离之和变小。当P==Q时为最优解。

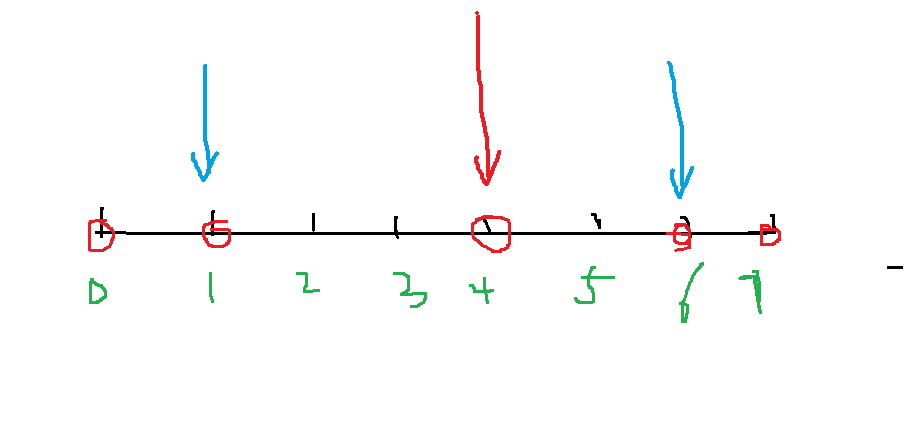
结合图片，红色的圈表示商店，蓝色的箭头表示仓库的所在地：

  • 第一种情况：左边的商店数目小于右边时，往右移动，则左边的都要加一，右边的都要减一，而右边的多，所以最终距离和会变小！
  • 第二种情况：左边的商店数目大于右边时，往左移动，则左边的都要减一，右边的都要加一，而左边的多，所以最终距离和会变小！
  • 第三种情况：第一种情况左移，和第二种情况右移，会发现最终都是变大的！

总结：仓库的位置一定不在靠左，也不在靠右，因为，如果在两边，都会有更优的地方，可以取到最小值！所以中间一定是最优的地方；

也就是上图的红色箭头处，五个仓库取中间即可！

分一下奇偶数情况，都进行取中位数即可，即仓库从N个商店中找一个中间商店，若为偶数则随便即可！我们统一选择偶数时编号小的那个：即res = n- 1 >> 1

一篇好理解一点的题解：点击这里！

题解：

题解一：（TLE）超时代码

时间复杂度：O(N2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
int a[N], b[N], k;

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++) cin >> a[i];
    sort(a, a + n);
    int res = 0x3f;
    for(int i = a[0]; i < a[n - 1]; i++)
    {
        int sum = 0;
        for(int j = 0; j < n; j++)
        {
            sum += abs(i - a[j]);
        }
        b[k++] = sum;
    }
    sort(b, b + k);
    cout << b[0] << endl;
	return 0;
}

题解二：选取中位数为仓库处

时间复杂度：O(N)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
int a[N];

int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i++) cin >> a[i];
    sort(a, a + n);
    int 
    int sum = 0;
    for(int i = 0; i < n; i++)
        sum += abs(a[res] - a[i]);
    cout << sum << endl;
	return 0;
}