首先来首歌曲来放松一下吧！

题目链接：99. 激光炸弹

题目背景：

题目描述

地图上有 N 个目标，用整数Xi,Yi表示目标在地图上的位置，每个目标都有一个价值Wi。

注意：不同目标可能在同一位置。

现在有一种新型的激光炸弹，可以摧毁一个包含 R×R 个位置的正方形内的所有的目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和x，y轴平行。

若目标位于爆破正方形的边上，该目标不会被摧毁！

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式

第一行输入正整数 N 和 R ,分别代表地图上的目标数目和正方形的边长，数据用空格隔开。

接下来N行，每行输入一组数据，每组数据包括三个整数Xi,Yi,Wi,分别代表目标的x坐标，y坐标和价值，数据用空格隔开。

输出格式

输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围

0≤ R ≤109
0< N ≤10000
0≤ Xi,Yi ≤5000
0≤ Wi ≤1000

输入样例：

1
2
3
2 1
0 0 1
1 1 1

输出样例：

1
1

题目分析：

题目要求：

就是在一个地图上放一个边长为 r 正方形，最后要输出这个正方形扣住的区域权值最大的值！

注意：正方形的边上的不算！

解题思路：

首先引入一维前缀和：

作用：可以在O(1)的时间内求出某一段区间的和！

举个例子：

a[1]、a[2] … a[n]

引入s[i]前缀和：

s[i] = s[0]…+s[i]

加入求a[7] ~ a[40] 那么就等于s[40] - s[6]！

接着引入二维前缀和：

就是变成了一个坐标：

首先给出递归式：s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

画个图：紫色的自己加上红色和绿色构成的矩形，再加上另一个红色和绿色构成的矩形，在减去多加的绿色部分！

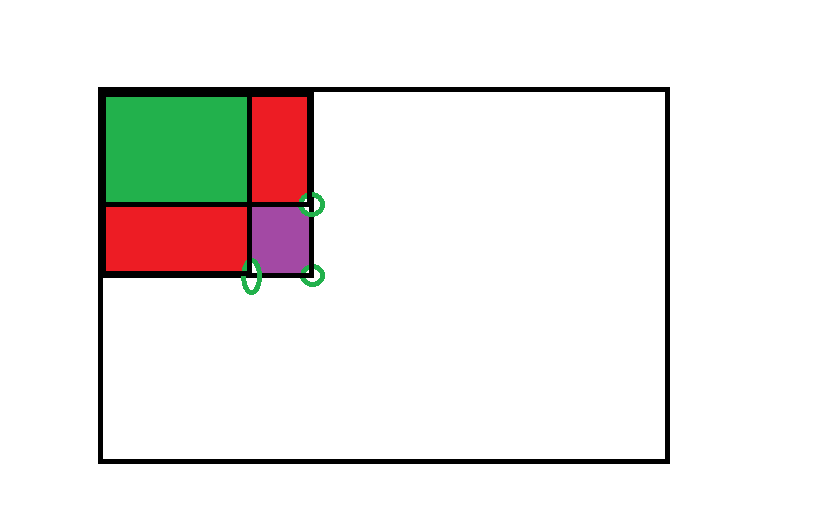
接下来开始预处理前缀和，在输入是让x和y都加了1，这样在预处理时，不会出现负数下标，免得处理边界问题！

由于每个点不止一个目标：所以数组要进行累加：g[x][y] += w;

接下来开始划分边长为R的矩形，要保证边长足够，所以i和j 最小也得从R开始，此时的(i, j) 指向的是矩形的右下角，这样可以保证不越界！

递推式：g[i][j] - g[i - r][j] - g[i][j - r] + g[i - r][j - r]

很好理解的：此时的(i , j)表示的行和列，即第i行第j列！

如下图：

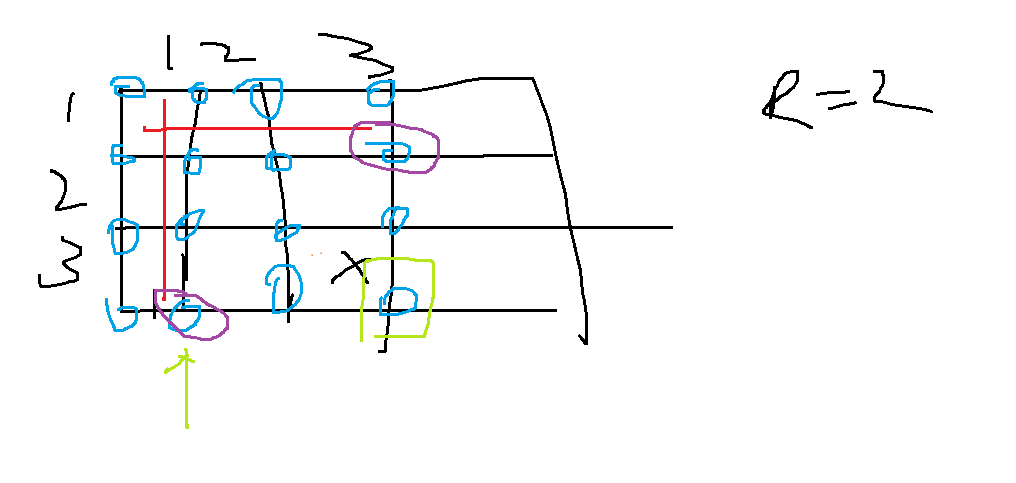
假如：r = 2,要计算 g[3][3]为右下角时，需要减去画那两道红线所构成的两个矩形，再加上多减掉的交叉部分，这样剩下的就是从青绿色右下角开始的四个蓝色的圈，这样看来，得到的结果就不是R 边长了，而是R- 1的边长，这样也就可以保证边上的不被计算！

为什么不把右边和下边两条边也删掉了？

我看了好久！才发现：

不能删，删掉上和左就够了！

你可以在脑袋里想一下，将那个矩形在图上飘起来，会发现盖住的部分最多就是那四个蓝色的圈！而R - 1 就可以实现边上的不记录效果！

好好理解一下，可能有点绕！

yxc大神视频讲解：点击这里！

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>

using namespace std;

const int N = 5010;
int g[N][N];

int main()
{
	int s, r;
	cin >> s >> r;
	// 题目R的数据有点问题，怎么可能比坐标最大还打，所以约束一下
	r = min(r, 5010);
	
	int n = 5010;
	
	for(int i = 0, x, y, w; i < s; i++)
	{
		cin >> x >> y >> w;
		x ++, y ++;
		g[x][y] += w;
	}
	// 预处理前缀和
	for(int i = 1; i < n; i++)
		for(int j = 1; j < n; j++)
			g[i][j] += g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1];
	
    // 找到（i，j）为矩形右下角
	int res = 0;
	for(int i = r; i < n; i++)
		for(int j = r; j < n; j++)
			res = max(res, g[i][j] - g[i - r][j] - g[i][j - r] + g[i - r][j - r]);
	
	cout << res << endl;
	
}