AcWing-89.a ^ b

¶首先来首歌曲来放松一下吧！

题目链接：89. a^b

¶题目背景：

¶题目描述

求 a 的 b 次方对 p 取模的值。

¶输入格式

三个整数 a,b,在同一行用空格隔开。

¶输出格式

输出一个整数，表示a^b mod p的值。

¶数据范围

0≤a,b,p≤10⁹

¶输入样例：

3 2 7

¶输出样例：

¶题目分析：

¶题目要求：

求a 的 b 次方模 p 的值。

¶解题思路：

直接循环求a 的 b 次幂，很明显会超时，C++ 一秒大概能运行10的7次方到10的8次方次之间，本题数据为10的9次方，肯定超时！

所以需要用到快速幂来计算：

快速幂思想如图：

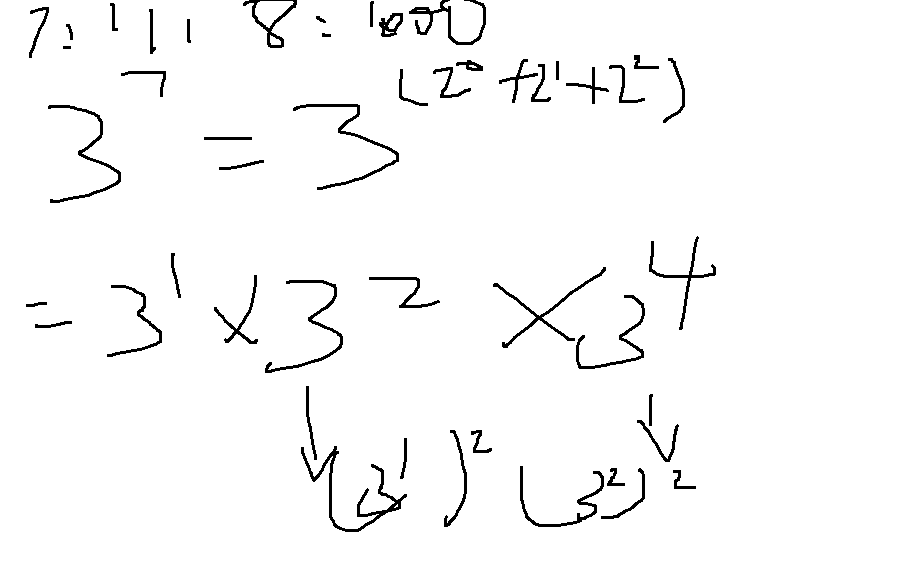
假如计算3 的 7 次方，7的二进制为111，如图，3的7次相当于3的1次，2次，4次，即3的2的0次+1次+2次，而3的2次是3的1次的平方，4次是2次的平方，所以这样看来，7次本来要算7回，这样只需要算三次即可，当然这里数据较小，假如是3的1000000次，只需要计算20次左右！可见提高了多少速度。

具体思想：对次数取最后一位，如果是奇数（即对应二进制位为1），就去累乘，如果是偶数（即二进制位为0），就跳过；当然每次都要存储好下一次需要计算的数据，即将当前值平方即可！

yxc大神的快速幂模板，点击这里！

yxc大神的视频讲解，点击这里！

¶题解：

注意点：

如果数据是这样：9 0 1 ，此时while进不去，最后会输出初始值1，但结果要对1取余，所以应该是0！所以要在开始时就对res 取余，次数取余不会影响到后面计算，只要p 比1大，此处相当于没有变化，只有1的时候会变化！或者也可以用if 来判断一下即可！
b&1 ：就是判断是不是奇数，或者说对应的二进制位是不是1
1ll ：可以简单的将数据转化为long long类型，以防溢出！
b >> 1 ：即二进制位右移，相当于除2，转化为二进制位就是将最后一位扔掉！

#include <iostream>

using namespace std;

int a, b, p;
long long res = 1;

int main()
{
    cin >> a >> b >> p;
    res %= p;
    while(b)
    {
        if(b&1) res = res * 1ll * a % p;
        a = a * 1ll * a % p;
        b >>= 1;
    }
    cout << res << endl;
    return 0;
}