题目链接：LeetCode 456. 132模式

这是一道非典型的单调栈问题！

一、题解

先来简单分析一下该题：

就是找是否有满足如下条件的数 i < j < k 并且 nums[i] < nums[k] < nums[j]，对于本题，我们可以从暴力角度考虑，即三层for循环，但实在是过于暴力，于是乎就产生了一个新的想法：

我们可以枚举每个nums[i]，对于每个nums[i]，判断其后是否有一个慢如如下要求的nums[k]：

  • nums[k] > nums[i]
  • nums[i] 和 nums[k] 之间存在一个 nums[j] 且 nums[j] > nums[k]

对于如上要求的nums[k]，我们可以进行转化：

即只要找到满足要求（所谓满足要求，这里是指上面的两个要求都满足）的nums[k]中最大的nums[k]即可！

即此时的nums[k]是大于nums[i]的数且比num[j]小的数中的最大的数！

而这样的数一定满足要求！

  • 如果有这样的数，则本题有解，否则无解

那么，如何求得满足要求的最大的 nums[k] 呢？

这里就要用到单调栈的知识了，但求这样一个数又和单调栈的经典定义不太一样，这便是这道题的难点！

经典的单调栈的为：在一个序列中可以求出左边第一个比他小或右边第一个比他小，左边第一个比他大或右边第一个比他大的数！

很明显，则并不是一个经典的单调栈问题！

  • 我们用一个栈stk来存储当前未满足要求的nums集合！我们会惊奇的发现 ，未满足要求的集合是单调的！ 这时，可以我们就可来维护一个未满足条件的单调栈来解题！
  • 我们用一个right_max数组来存储当前当前数右边比他大的最大的数，即满足要求的数

若存在right_max，使得nums[i] < right_max，即可说明存在一个132序列，否则说明无解！

还有一个比较容易困惑的事情：

  • 当前得到的right_max并不是给当前的nums[i]使用的，而是给下一次循环的nums[i]之前的nums[i - 1]使用的！
  • 即 num[i - 1] num[i] right_max三者为i,j,k的关系，right_max会在下一层循环num[i - 1]时候会用到，这时候已经保证了nums[j] > nums[k]，且nums[k]取到最大的条件了！

如何维护该单调栈呢？

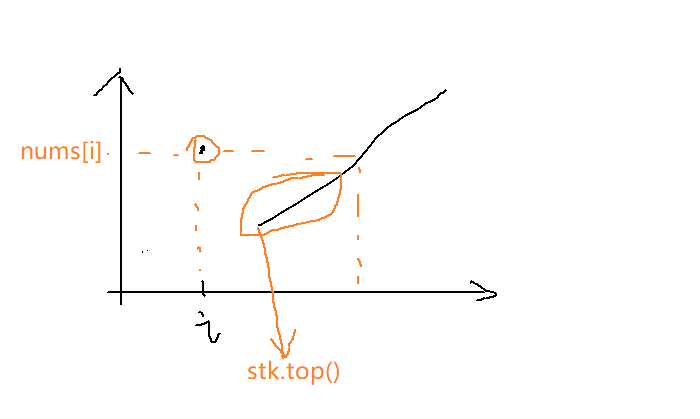
对于当前的nums[i]（此时的nums[i]就是132序列的nums[j]）来说，若栈中有元素比当前nums[i]要小，我们要取到比nums[i]小的区间内的最大值，因此，该区间就可以被删去，只要该最大值存在，那么栈中该区间中的任意值就都不会被使用到！

时间复杂度：O(n)

空间复杂度：O(n)

二、AC代码

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool find132pattern(vector<int>& nums) {
        stack<int> stk;
        int right_max = INT_MIN;
        for(int i = nums.size() - 1; i >= 0; i --){
            if(nums[i] < right_max) return true;
            while(stk.size() && stk.top() < nums[i]){
                right_max = max(right_max, stk.top());
                stk.pop();
            }
            stk.push(nums[i]);
        }
        return false;
    }
};