题目链接：AcWing 131. 直方图中最大的矩形

这道题自然就是非常典型的单调栈问题！

一、题解

该题目如下图：找一个最大的矩形出来！

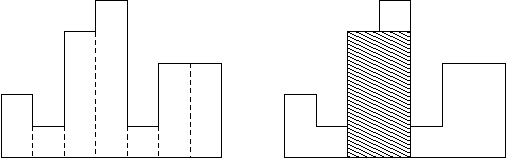
有了前面单调栈知识的积累，会轻易的发现这道题就是一道单调栈的应用！

我们看图可以知道，以其中一个矩形的顶部作为一条边，那么他向左和向右最大能拓展的长度就是他的宽度！最终面积就是能拓展的最大宽度乘以该矩形的高就是以该矩形顶部为边的最大矩形！每个矩形都枚举一次即可得到最大矩形的面积！

问题来了，如何快速找到该矩形向左和向右最远能拓展到哪里呢？

其实，这个问题换句话说就是，如何可以快速的找到左边或右边第一个比他低的矩形的位置！

现在可以发现了吧！

这就是单调栈的定义呗！

具体操作：

  1. 从左到右维护一个单调栈，从右到做维护一个单调栈即可！
  2. 由于要维护两次，为了方便我们使用自己实现的栈结构q
  3. l r数组分别表示左边或右边第一个比他矮的矩形的下标位置
  4. 最终面积就是h[i] * (r[i] - l[i] - 1)

注意点：

  • 本题数据大，可能爆int，使用long long强转一下！
  • 两次扫描之间，记得清空栈
  • 为了便于处理边界数据，从1 - n进行循环
  • 边界数据h[0], h[n + 1]为-1
  • 左右边界q[0]所代表的的下标的值分别为0和n + 1

时间复杂度：O(n)

空间复杂度：O(n)

二、AC代码

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int n, h[N], l[N], r[N], q[N];

int main(){
    while(cin >> n, n){
        
        for(int i = 1; i <= n; i ++) cin >> h[i];
        
        int tt = 0; q[0] = 0, h[0] = -1;
        for(int i = 1; i <= n; i ++){
            while(h[q[tt]] >=  h[i]) tt --;
            l[i] = q[tt], q[++ tt] = i;
        }
        
        tt = 0, q[0] = n + 1, h[n + 1] = -1;
        for(int i = n; i >= 1; i --){
            while(h[q[tt]] >= h[i]) tt --;
            r[i] = q[tt], q[++ tt] = i;
        }
        
        LL res = 0;
        for(int i = 1; i <= n; i ++) res = max(res, (LL)h[i] * (r[i] - l[i] - 1));
        cout << res << endl;
    }
    return 0;
}