首先来首歌曲来放松一下吧!
题目链接:106. 动态中位数
题目背景:
让两个堆来构建一个有序序列,找到中位数,优先队列的优先就是用堆结构实现的!
题目描述
依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。
输入格式
第一行输入一个整数P,代表后面数据集的个数,接下来若干行输入各个数据集。
每个数据集的第一行首先输入一个代表数据集的编号的整数。
然后输入一个整数M,代表数据集中包含数据的个数,M一定为奇数,数据之间用空格隔开。
数据集的剩余行由数据集的数据构成,每行包含10个数据,最后一行数据量可能少于10个,数据之间用空格隔开。
输出格式
对于每个数据集,第一行输出两个整数,分别代表数据集的编号以及输出中位数的个数(应为数据个数加一的二分之一),数据之间用空格隔开。
数据集的剩余行由输出的中位数构成,每行包含10个数据,最后一行数据量可能少于10个,数据之间用空格隔开。
输出中不应该存在空行。
数据范围
1≤P≤1000
1≤M≤9999
输入样例:
1
2
3
4
5
6
7
8
9
| 3
1 9
1 2 3 4 5 6 7 8 9
2 9
9 8 7 6 5 4 3 2 1
3 23
23 41 13 22 -3 24 -31 -11 -8 -7
3 5 103 211 -311 -45 -67 -73 -81 -99
-33 24 56
|
输出样例:
1
2
3
4
5
6
7
| 1 5
1 2 3 4 5
2 5
9 8 7 6 5
3 12
23 23 22 22 13 3 5 5 3 -3
-7 -3
|
题目分析:
题目要求:
输入一串数,在输入奇数位时,输出当前序列的中位数!
解题思路:
本人的暴力做法:
每次输入一个数,就使用sort来拍一下序,为奇数位时,输出当前的中位数!
看看时间复杂度:1e3 * 1e4 * NlogN 大概已经1e11 绝对TLE!
更优的做法:使用对顶堆
时间复杂度:1e3 * 1e4 * logN
似乎是这样!不太会分析复杂度。。。
使用两个堆结构:大根堆和小根堆,且必须时刻满足这两个条件!
- 大根堆:序列中从小到大排序为 1 ~ M / 2 个数存储到大根堆
- 小根堆:序列中从小到大排序为 M + 1~ M 个数存储到大根堆
始终保证大根堆元素小于小于等于小根堆,小根堆元素大于等于大根堆元素个数!
输入一个数先进行存储,若比中位数小,存储到大根堆,比中位数大存储到小根堆!
倘若不符合上面两个条件:
需要进行多的给少的,达到上面的限制条件即可!
为什么要这样限制了?
看一下这张图:
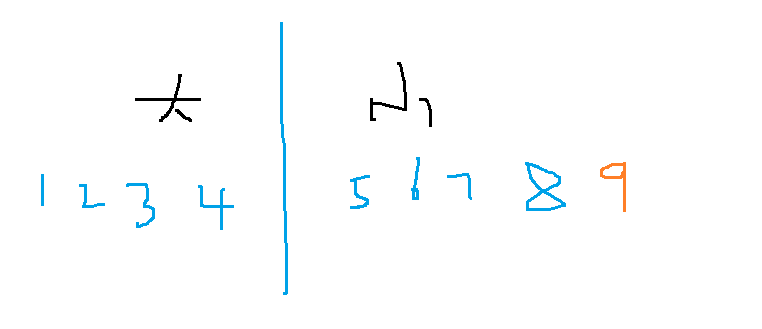
会发现每次插入结束后,只要保证右边大于等于左边,就可以轻而易举得到中位数,就是小根堆的堆顶!
如果是偶数个数,则左右是相等个数,若为奇数,则右边一定会多一个!
以这几个数举例:没有9时,则中位数为5?不对吧,没关系,题目要求在奇数个数时去找中位数,所以右边一定比左边多1,这时,也就是有9的时候,中位数就是5,没毛病!
大根堆的堆顶为4,小根堆的堆顶为5 !
具体实现请看下方代码!
李煜东的视频讲解,大概在45分钟的时候!
题解:
题解一:本人的纯暴力做法!(TLE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010;
int a[N], b[N];
int p, q, n;
int main()
{
cin >> p;
while(p --)
{
cin >> q >> n;
int k = 0;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
sort(a + 1, a + 1 + i);
if(i & 1) b[k++] = a[i + 1 >> 1];
}
cout << q << " " << k << endl;
for(int i = 0; i < k; i++)
{
if(i % 10 == 0 && i) cout << endl;
cout << b[i] << " ";
}
cout << endl;
}
return 0;
}
|
题解二:使用对顶堆(大根堆和小根堆)(AC)
注意:将第一个数直接插入小根堆,毕竟要保证右边大于等于左边!
在清空堆的时候,由于没有clear函数,只能使用循环去删除达到空容器效果,或者直接赋值一个空容器,建议使用赋值方法!简单明了,vector可以直接使用clear函数清空!
关于优先队列:
默认为大根堆,要使用小根堆得如代码这样写,很明显第三个参数为排序函数!
1
2
| priority_queue <int> big, kong1;
priority_queue <int, vector<int>, greater<int> > small, kong2;
|
具体代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include <queue>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10010;
int p, q, n;
vector <int> v, kongV;
priority_queue <int> big, kong1;
priority_queue <int, vector<int>, greater<int> > small, kong2;
int main()
{
cin >> p;
while(p --)
{
cin >> q >> n;
int k = 0;
big = kong1, small = kong2, v.clear();
for(int i = 1, x; i <= n; i++)
{
cin >> x;
if(small.empty())
{
small.push(x);
v.push_back(x);
continue;
}
if(x >= small.top()) small.push(x);
else big.push(x);
if(big.size() > small.size())
{
small.push(big.top());
big.pop();
}
else if(small.size() - big.size() > 1)
{
big.push(small.top());
small.pop();
}
if(i & 1) v.push_back(small.top());
}
cout << q << " " << v.size() << endl;
for(int i = 0; i < v.size(); i++)
{
if(i % 10 == 0 && i) cout << endl;
cout << v[i] << " ";
}
cout << endl;
}
return 0;
}
|
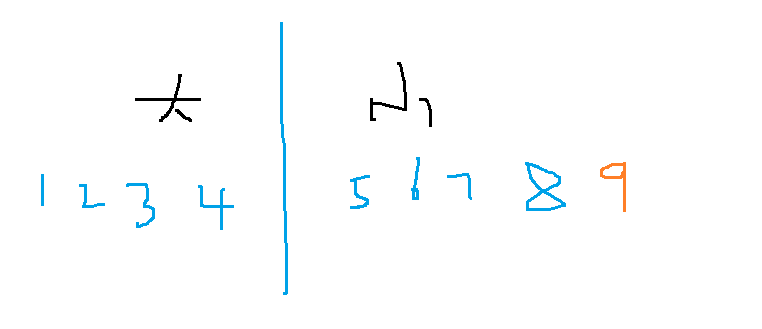




.jpg)
.jpg)