题目链接：42.接雨水

题解：

多种做法，第一次接触确实有点难，单调栈的应用，以及双指针这个神奇算法的应用！

计算这种面积，不要瞎想，大概两种，一种计算纵向，一种计算横向！

下面三种解法，推荐去看双指针和单调栈，学习算法，尽可能多的一题多解，双指针解法是最优的，但是单调栈也是一种思想，多学点没坏处！

题目简述：

接雨水，给定一堆柱子，问柱子之间的凹槽最多放多少水！如下图：蓝色部分就是最多的接水量。

题解一：三次扫描

计算纵向：即每个柱子上方可以存水的量，累加即可！

如何计算？

观察会发现，当前柱子能存的水取决于当前柱子左边最高的柱子和当前柱子右边最高的柱子，由于短板效应，所以能存的水为左右两边最高的柱子的较小值与当前柱子高度的差值。

如何计算左右最高的柱子？

简单办法：直接扫描一遍即可，使用两个数组保存该位置左右的最高柱子，left_max[i]表示i位置（包括自己）的柱子左边的最高柱子，同理right_max[i]表示i位置（包括自己）右边最高柱子。一个从左向右扫描维护该数组，一个从右向左扫描维护该数组即可。

第三次扫描，直接计算每个柱子的可存水的高度即可！即min(left_max[i], right_max[i]) - height[i]

注意：因为要进行动态维护，要和前一个最大值比较，所以数组left_max从1开始，right_max从n - 1开始。

时间复杂度： 三次线性扫描，为 O(n)

空间复杂度： 开辟了两个额外数组，空间占用为 O(n)

注意：判断为空的情况！

为什么要扫描三次，一次扫描不行吗？

答案是可以，使用双指针来维护！详见题解二！

AC代码一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size(), res = 0;
        if(n == 0) return 0;
        
        vector<int> left_max(n), right_max(n);
        left_max[0] = height[0];
        for(int i = 1; i < n; i++) left_max[i] = max(left_max[i - 1], height[i]);

        right_max[n - 1] = height[n - 1];
        for(int i = n - 2; i >= 0; i--) right_max[i] = max(right_max[i + 1], height[i]);

        for(int i = 0; i < n; i++) res += min(left_max[i], right_max[i]) - height[i];
        return res;
    }
};

题解二：双指针

同样是计算纵向！

使用双指针，一次扫描，不用多余的空间！

首先：思想就是一个桶能装多少水，一定是由短板决定的，所以我们就是根据这句话来想，我们不去找左右最大值，直接找短板即可！

当前算法过程就是不断的计算左柱子和右柱子，直到左右相碰结束！

具体解法：

  1. 使用l和r分别指向左右两个指针
  2. 使用left_max和right_max分别指向l左边最大值和r右边最大值
  3. 左边最大值小于右边最大值时，即left_max < right_max，说明height[l]这根柱子的短板已经找到，为left_max，当前总面积累加为res += left_max - height[l]
  4. 然后左指针右移，l++
  5. 更新left_max，即left_max = max(left_max, height[l])
  6. 左边最大值大于等于右边最大值时，同理！

具体解释：

为什么左最大小于右最大，即为左柱子的短板；为什么右最大小于左最大，即为右柱子的短板？

还是短板效应！ 如果左最大小于右最大，左边柱子的赛点就到了，左边最大即为当前柱子的短板！你想啊，虽然两个指针中间还有未走完的路，但是右边的最大值一定会在后续更新到更大，不管怎样，相比之下，左右最大值中的最小值一定是当前左边的最大值。同理右边较小时也是！

时间复杂度： l 和 r一共扫描一遍数组，为 O(n)

空间复杂度： 没有使用额外空间，空间占用为 O(1)

注意：判断为空的情况！

AC代码二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 双指针 时间 O(n) 空间 O(1)
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size(), res = 0;
        if(n == 0) return 0;

        int left_max = height[0], right_max = height[n - 1];
        int l = 0, r = n - 1;
        while(l < r){
            if(left_max < right_max){
                res += left_max - height[l++];
                left_max = max(left_max, height[l]);
            }else{
                res += right_max - height[r--];
                right_max = max(right_max, height[r]);
            }
        }
        return res;
    }
};

题解三：单调栈

计算横向！

我是第一次接触单调栈！

本题可以使用单调栈，所谓单调栈就是具有单调性的栈。。。

为了存到水，那么一定要有凹槽，即左边下去，右边起来，我们用栈来维护左边下去的这一段，即当前栈是一个单调递减的栈！

如下图： 我们在栈中存储左边那四根递减的柱子！

具体算法：

  1. 有了凹槽才需要计算面积，所以，递减的栈要找到大于栈顶的位置才需要计算面积。
  2. 首先出栈栈顶并将其记为top，然后当前stk.top()、top、i就构成了一个凹槽，可以进行一次计算，
  3. 即红色块面积，宽度为i - stk.top() - 1，高度为min(height[i], height[stk.top()]) - height[top]
  4. 算完后while结束，继续下一次for循环，i后移，严格保证栈的单调性
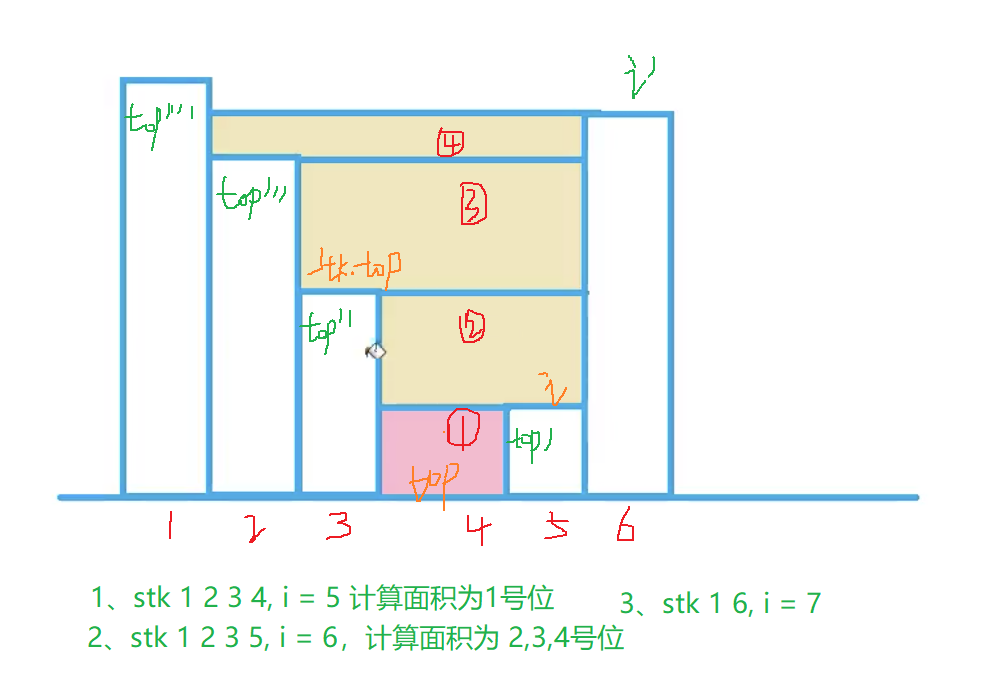
  5. 此时栈又不单调了，进行处理，此时i到了i'，会发现多出了黄色三个矩形块的面积，2,3,4号矩形，可以在while内循环全部干掉，边干边出栈，最后栈内为1,6
  6. 每次while循环结束，将当前位置 i压入栈内。

具体看下方图理解一下，这里维护了一个单调栈，永远单调，遇到凹槽就进行计算累加，横向的面积！

注意：如果出栈一次后，栈空，即当前的形状不是凹槽，就像当前只有top和i一样，无法存水，break即可！

时间复杂度： 扫描一次，为 O(n)

空间复杂度： 栈开辟了一个数组，空间占用为 O(n)

AC代码三：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 单调栈 时间O(n) 空间O(n)
class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk;
        int res = 0;
        for(int i = 0; i < height.size(); i++){
            while(stk.size() && height[stk.top()] < height[i]){
                int top = stk.top(); 
                stk.pop();
                if(stk.empty()) break;
                res += (i - stk.top() - 1) * (min(height[i], height[stk.top()]) - height[top]);
            }
            stk.push(i);
        }
        return res;
    }
};