LeetCode刷题-89. 格雷编码
题目链接:89. 格雷编码
¶题解:
一个有趣的题,做法也是特殊的,需要记住!
¶题目简述:
格雷编码是一个二进制数组合,每两个二进制数对应位数只能有一位不同,所有的组合对应的数集合称之为格雷编码!
给定一个数,为二进制位数,返回该位数的格雷编码集合!
¶题解:
特殊题目: 特殊做法,记住即可!
思路:
n位二进制,共有2^n种组合!
- 先将n-1位的二进制位,上下轴对称,再将轴上方的最后补0,轴下方的最后补1即可!
如下图:
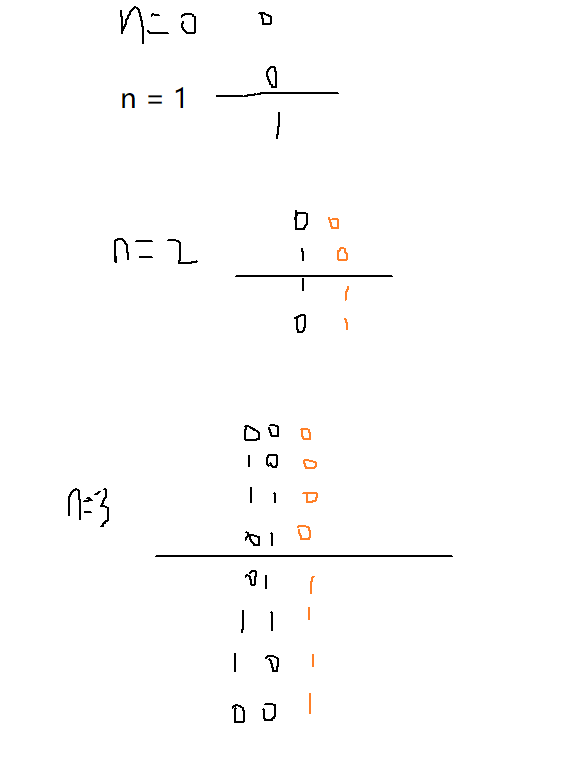
简单解释一下正确性:
- 对
n - 1来说,已经满足格雷编码性质,现在来看n的情况: - 对于轴上部分,原来相邻的都差一位不同,在最后都加一个相同的
0则还是相邻之间差一位 - 对于轴下部分,原来相邻的都差一位不同,在最后都加一个相同的
1则还是相邻之间差一位 - 对于轴上下相邻部分,由于轴对称,原来是完全一致的,现在一个加
0,一个加1,也满足差一位的性质
对于数组具体存储数字的处理:
- 轴上的部分在最后加0,相当于整体左移一位,即
res[i] *= 2 或 res[i] << 1,没有产生新数据,原数据发生改变 - 轴下的部分在最后加1,相当于原数加1产生的新数假如数组末尾,即
res.push_back(res[i] + 1) - 当然,对轴下部分的处理的顺序和图片上的不一致,如果对第一个数加1,相当于轴下的最后一个数,从图上来说,即轴下的新数据是从下往上添加到数组末尾的,产生了新的数据
初始转态: 为n = 0时候,数组只要一个0.
时间复杂度:对于给定的n,计算量为:1 + 2 + 4 + 8 + … + 2^n-1 = 2 * (2^n-1 - 1) = 2^n - 2,即O(2^n)
¶AC代码:
1 | |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 小牛博客!
评论




