题目链接：33.搜索旋转排序数组

题解：

开始进入二分的时代，二分模板要掌握并理解。

题目简述：

一个升序序列在某一点反转形成两个升序序列，从其中找到一个目标值，不存在返回 -1，要求时间复杂度为O(log n)级别。

题解：

自然而然的想到要使用二分了！

二分的二段性：一段满足，另一段不满足，则可以将分界点二分出来！

二分可以找到满足条件的最后一个数！最后（指的是按照区间缩小的趋势最后满足条件的数）

二分模板：点击这里！

注意：关于mid加不加一的问题，若 l= mid就得加，否则只有两数会造成死循环；若r = mid就不能加，否则只有两数也会造成死循环。

‘

本题分为了两段，根据二分的二段性，当 x >= nums[0]的时候，会发现左边一段都符合条件，右边一段都不符合条件，可以使用二分，二分到分界点。

如下图：

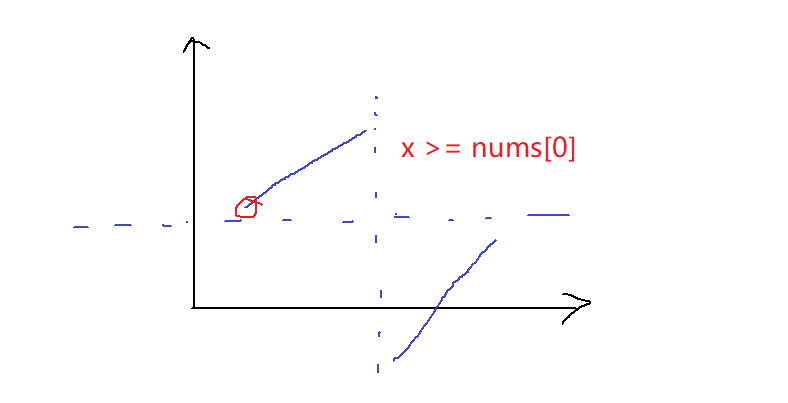
找到分界点后，判断当前目标值在哪一段，继续进行二分即可！

  • 0 ~ mid
  • mid + 1 ~ nums.size() - 1

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.empty()) return -1; // 0 1
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + r + 1 >> 1;
            if(nums[mid] >= nums[0]) l = mid;
            else r = mid - 1;
        }

        if(target >= nums[0]) l = 0;
        else l = r + 1, r = nums.size() - 1;

        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if(nums[r] == target) return r;
        else return -1;
    }
};