题目链接：30.串联所有单词的子串

题解：

嗯，有点难度，使用哈希表和分类的思想！

题目简述：

给定一个字符串，一个字符串数组，从字符串中找出可以包含字符串数组左右元素的起始位置！

题解：

暴力：不推荐

这里直接采用高效率的算法：

预先规定：

n = s.size(), m = words.size(), w = words[0].size();

使用分类思想：

本题可以划分为w类，如下图所示：

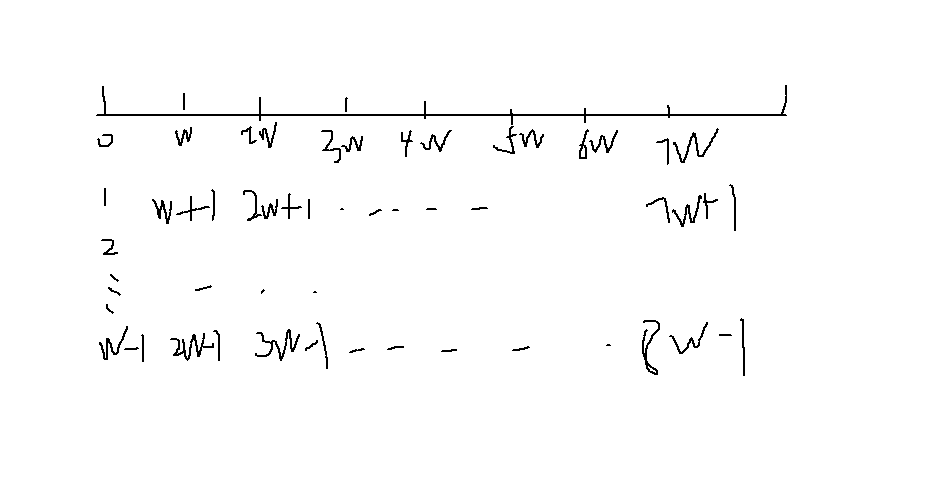
可以发现，可以把起点分为0 - w-1的w组，你会惊奇的发现，起点从w-1往后，都已经被前面的情况所包括了！

而且，我们扫描时按单词的长度w往后走，即每个单词一定落在坑里！

具体做法：

使用一个哈希表tot记录words数组中单词出现的数量，使用另个一个哈希表wd 动态 记录选定区间的单词数量。

当两个哈希表单词和数量对应相等时即匹配了一组，继续后续匹配。

怎样处理两个哈希表是否一致，暴力，复杂度太高，所以使用一个 动态 变量cnt，用来统计两个容器对应的个数！

当cnt == m时，即为找到了一组合法区间。

如何动态维护wd哈希表？

  1. 如果当前处理个数不到m，即j < i + m * w，则不需要进行哈希表的左端删除，只进行有端的添加，将当前单词substr(j, w)截取出来，wd[word]++进行统计：
    1. 若统计完以后，发现当前单词个数比需要的数量>= tot[word]，则说明当前单词不在tot中，不需要统计
    2. 否则，说明当前单词在tot容器中，cnt++
  2. 如果当前处理个数大于等于m个，即j >= i + m * w，则需要进行左端的删除和有端的添加，动态维护wd容器为m个单词。截取substr(j - m * w, w)第一个单词，wd[word]--进行统计：
    1. 若统计完以后，发现当前单词个数比需要的数量tot[word]要少，说明当前单词删除有效，删的在tot中，cnt--
    2. 否则说明，删除了一个不在tot中的单词，无序处理cnt
    3. 进行有端的添加，和第一步一样操作一模一样。
  3. 匹配条件：cnt == m即两个哈希表匹配成功，找到了一组合法区间一一对应，起始下标为j - (m - 1) * w

下标图解如下：

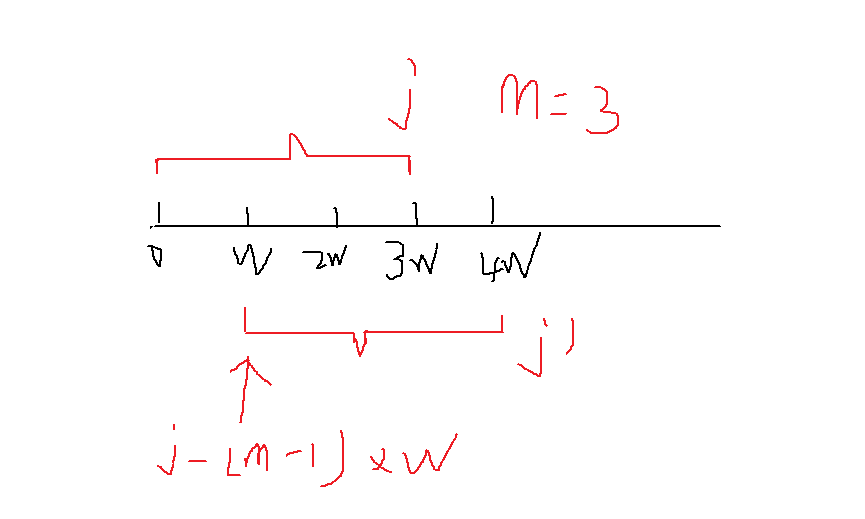
时间复杂度： 小区间个数为n / w，一共分为了w类，哈希表的插入删除复杂度为word长度w，总时间复杂度为O(n / w * w * w) = O(n * w)

进一步优化：

使用字符串哈希，可以将哈希表的插入删除降到O(1)，总时间复杂度降为O(n)。奈何没有学到，今后再学习，进行补充！

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> findSubstring(string s, vector<string>& words) {
        vector<int> res;
        if(words.empty()) return res;
        int n = s.size(), m = words.size(), w = words[0].size();
        unordered_map<string, int> tot;
        for(auto& word : words) tot[word]++;

        for(int i = 0; i < w; i++){
            unordered_map<string, int> wd;
            int cnt = 0;
            for(int j = i; j + w <= n; j += w){
                if(j >= i + m * w){
                    auto word = s.substr(j - m * w, w);
                    wd[word]--;
                    if(wd[word] < tot[word]) cnt--;
                }
                auto word = s.substr(j, w);
                wd[word]++;
                if(wd[word] <= tot[word]) cnt++;
                if(cnt == m) res.push_back(j - (m - 1) * w);
            }
        }
        return res;
    }
};