题目链接：28.实现strStr()

题解：

嗯，使用暴力就是简单题！

提高效率使用KMP，复杂了，好好理解，多实现，最好记住模板！本题就是一个模板。

题目简述：

给定两个字符串，从第一个中找第二个串，能找到返回起始下标，找不到返回-1，第二个串为空，直接返回0。

题解一：暴力

直接扫描一遍原串即可：

  • 先判断当前位置是否够子串的长度，不够直接返回-1，因为肯定没有可以匹配的。
  • 如果位置长度够，就从当前位置截取和子串长度相同，查看是否相等，相等直接返回当前下标i，否则继续下次循环

时间复杂度：substr(pos, m)：复杂度为O(len)，总时间复杂度为O(n*m)

AC代码一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty()) return 0;
        for(int i = 0; i < haystack.size(); i++){
            if(haystack.size() - i < needle.size()) return -1;
            if(haystack.substr(i, needle.size()) == needle)
                return i;
        }
        return -1;
    }
};

// 改一下这样可能更好。
class Solution {
public:
    int strStr(string haystack, string needle) {
        if(needle.empty()) return 0;
        for(int i = 0; haystack.size() - i >= needle.size(); i++)
            if(haystack.substr(i, needle.size()) == needle)
                return i;
        return -1;
    }
};

题解二：KMP

为了弄明白KMP算法，我也是盯着看，画着图搞了一上午！

这也是一个模板题，需要记下来并掌握代码的实现及理解该算法的运行流程！

时间复杂度： O(n + m)

为了方便，这里将字符串都从1开始！

1
s = " " + s, p = " " + p;

KMP算法的核心就是一个next数组：

next数组的作用：若没有该数组，后续匹配过程中出现不匹配的话，需要将起始位置后移一位，重新开始一一匹配，但是有了该数组，就不一定是移动一位了，而是移动尽可能多的位置，使得前j个字符和原串仍然匹配，只需判断第j + 1个字符即可！

首先搞清楚next数组存储的东西是什么？

next[i]： 所有s[1]-s[i]中前缀等于后缀的最大长度（特指非平凡前缀和后缀）

非平凡：指的是不包括自己，eg：abc中的next[3]不能为3，应该为0。

举个例子：

举个例子：abcdefghabcd中，next[12]就应该为4，即前缀和后缀相等的最大长度，为前缀abcd和后缀abcd匹配时的值。

下一个问题，怎么求next数组？

首先，next[0]不需要管，下标从1开始，next[1] = 0，非平凡不包括自己！

从下标为2开始即可！

假设当前状态如下：i - 1为原串p指向的位置，j为p的前缀后缀相等时前缀的尾。序号1和序号2是同一段，序号3是原串1 ~ (i - 1)中与前缀相等的后缀，此时序号1，2，3都是相等的。

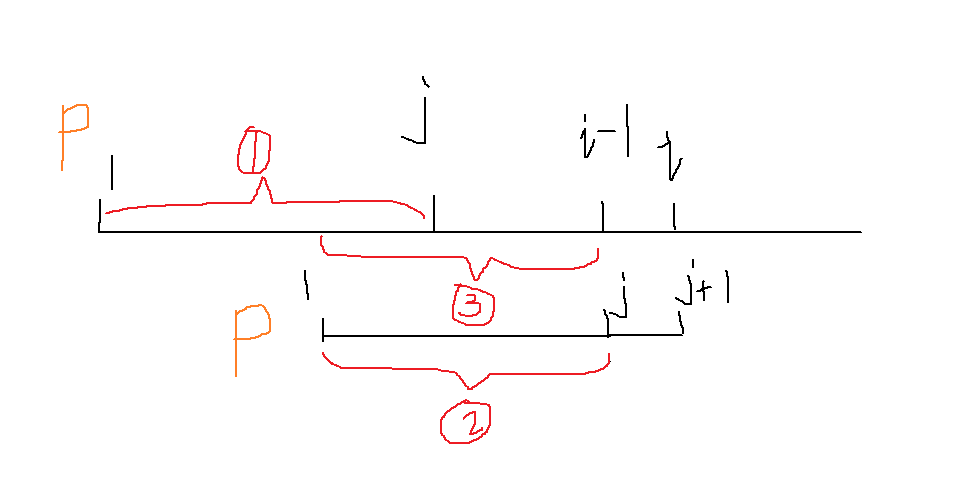
若 i 和 j + 1可以匹配，此时next[i]就会由j变为j + 1，则效果图如下：

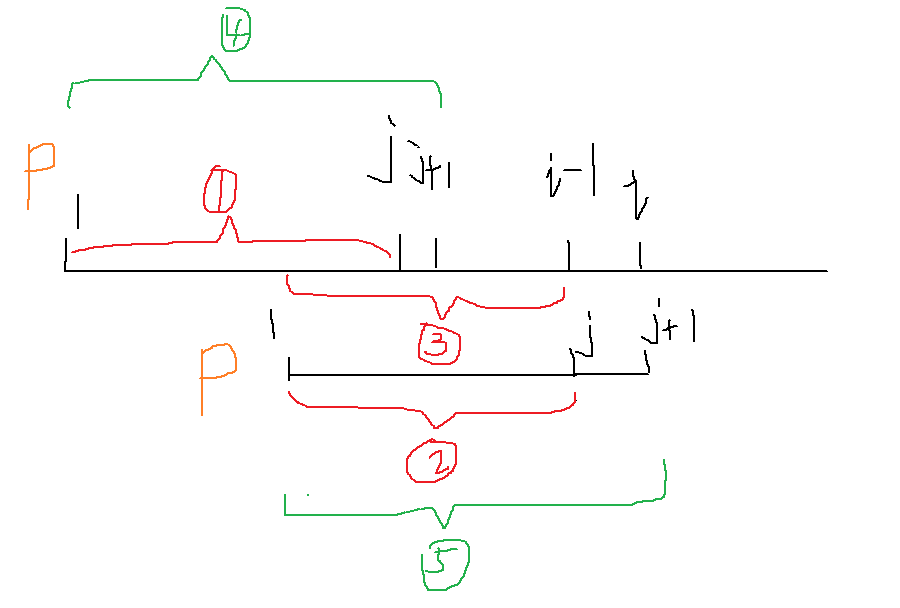
若 i 和 j + 1无法匹配，则说明前缀串1 ~ j无法满足当前next[i]的条件，此时j的位置就需要发生变化，将前缀缩小为1 ~ next[j]去试探此时是否可以匹配next[i]的条件，若一直无法匹配，已经到了next[1] = 0或j == 0时，仍然无法匹配，则当前next[i] = 0；若试探中，某次可以匹配，则当前next[i]的值就可以更新为当前next[j] + 1

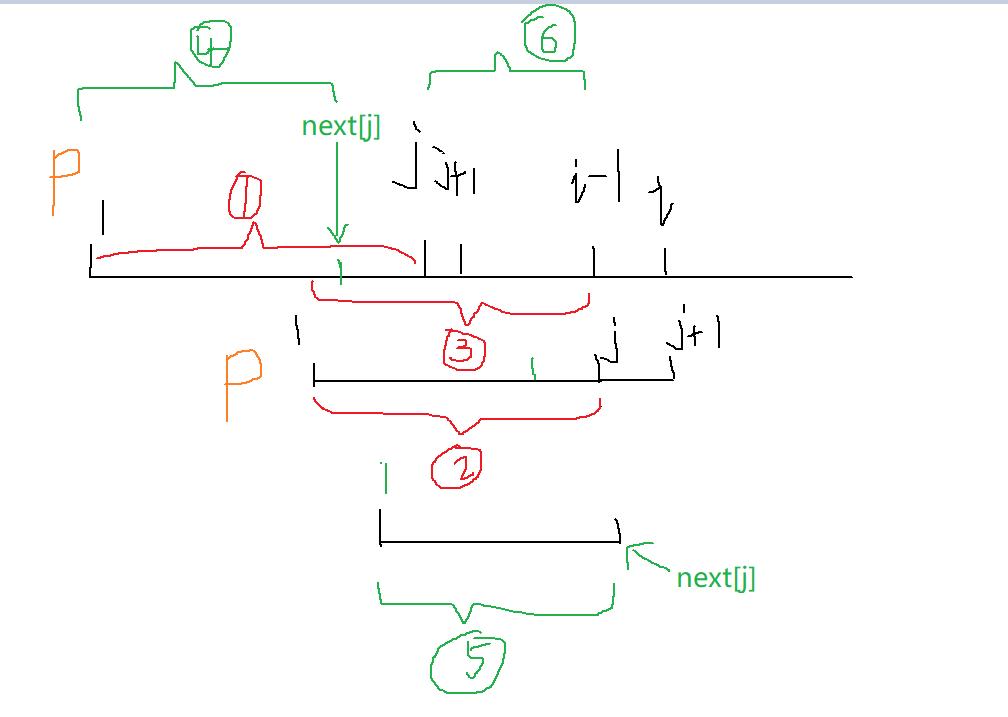
会发现后面的next计算都在前面已经算出来的基础上进行试探的，而前面算出来的都是前后缀相等且最长的，所以这样可以求得所有next数组的值，且一定是正确的！

下一个问题，怎么求子串与原串的匹配并计算得到起始下标？

和求解next数组一样，求解next数组是用的两个待匹配字符串p，求下面这个问题则只需要将第一个串换成s串即可，最后只需要判断什么时候等于待匹配字符串的长度，直接计算返回该下标即可！

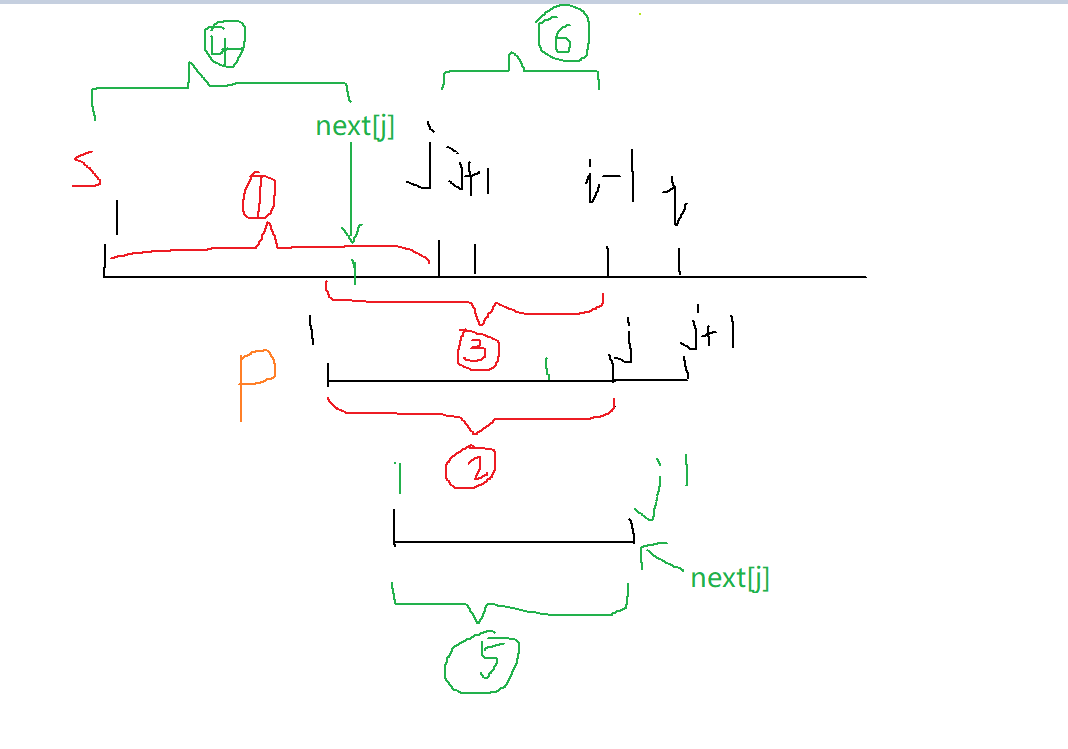
什么时候就算找到了？

当然是当j == m的时候，即说明此时已经匹配完了p串。

最终返回的长度就是i - m，即s串的匹配终点的前m个字符的位置，应该为i - m + 1，但是我们下标是从1开始，所以要减去1，i - m + 1 - 1即i - m。

注意：需要特判p串为空的情况，需要返回0。

AC代码二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int strStr(string s, string p) {
        if(p.empty()) return 0;
        int n = s.size(), m = p.size();
        s = " " + s, p = " " + p;
        vector<int> next(m + 1);
        for (int i = 2, j = 0; i <= m; i ++){
            while(j && p[i] != p[j + 1]) j = next[j];
            if(p[i] == p[j + 1]) j ++;
            next[i] = j;
        }

        for (int i = 1, j = 0; i <= n; i ++){
            while(j && s[i] != p[j + 1]) j = next[j];
            if(s[i] == p[j + 1]) j ++;
            if(j == m) return i - m;
        }
        return -1;
    }
};