首先来首歌曲来放松一下吧！

题目链接：4.寻找两个正序数组的中位数

题解：

此题 y总 的链接！

此题据 y总 说是LeetCode最难题目之一！

这个题目或许又可以称为

求解第k小数问题

题目简述：

两个有序序列，求中位数！

有一个很 优秀的要求：时间复杂度要控制在 O(log(m + n))

题解一：

先不看题目时间复杂度的要求：使用二路归并进行，时间复杂度O(n + m)

由于时间也不算太慢，还是可以AC的。题解二将使用更优秀的算法解决。

二路归并：思路，每次两两比较，将较小值放到新的容器。若某一个遍历完毕，则将没有遍历完的另一个一次放到新的容器。

本题奇偶两种情况处理，奇数位的中位数为 len > 1， 偶数位的中位数为 len > 1 和 (len > 1) - 1 和的均值！

注意点：返回值为double，所以记得乘以 1. 0 或除以 2.0

AC代码1：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        vector<int> nums3;
        int i = 0, j = 0;
        while(i < nums1.size() && j < nums2.size()){
            if(nums1[i] < nums2[j]) nums3.push_back(nums1[i++]);
            else nums3.push_back(nums2[j++]);
        }
        while(i < nums1.size()){nums3.push_back(nums1[i++]);}
        while(j < nums2.size()){nums3.push_back(nums2[j++]);}
        if(len & 1) return nums3[len >> 1];
        else return (nums3[len >> 1] + nums3[(len >> 1) - 1]) * 1.0 / 2;
    }
};

题解二：

由于题目要求时间复杂度为 O(log(n + m))，所有第一种解法不符合题意，虽然可以AC。

现在将给出第二种解法：使用递归分治

如何想到使用分治的呢？

时间复杂度为log级别的，想到 log 就会想到 除2，除2，除2 。。。。

所以本题采用类似思想，即每递归一次就将数据量减半，达到log级别！

具体实现：

递归函数的目的：在可选区间找到第 k 小的数 ，k > 0。

递归分治的思想：即将问题子问题化，由大变小，逐个解决。

本题求解：即求k = (n + m) / 2 的位置即可，使用递归求解 k / 2, k / 2 / 2.。。。。。直到k = 1，回溯到 k = (n + m) / 2的解，即为答案！

时间复杂度：O(log(k)) 即 O(log((n + m) / 2) 即 O(log(n + m))

好！

开始分解子问题：(k / 2)

简单图示

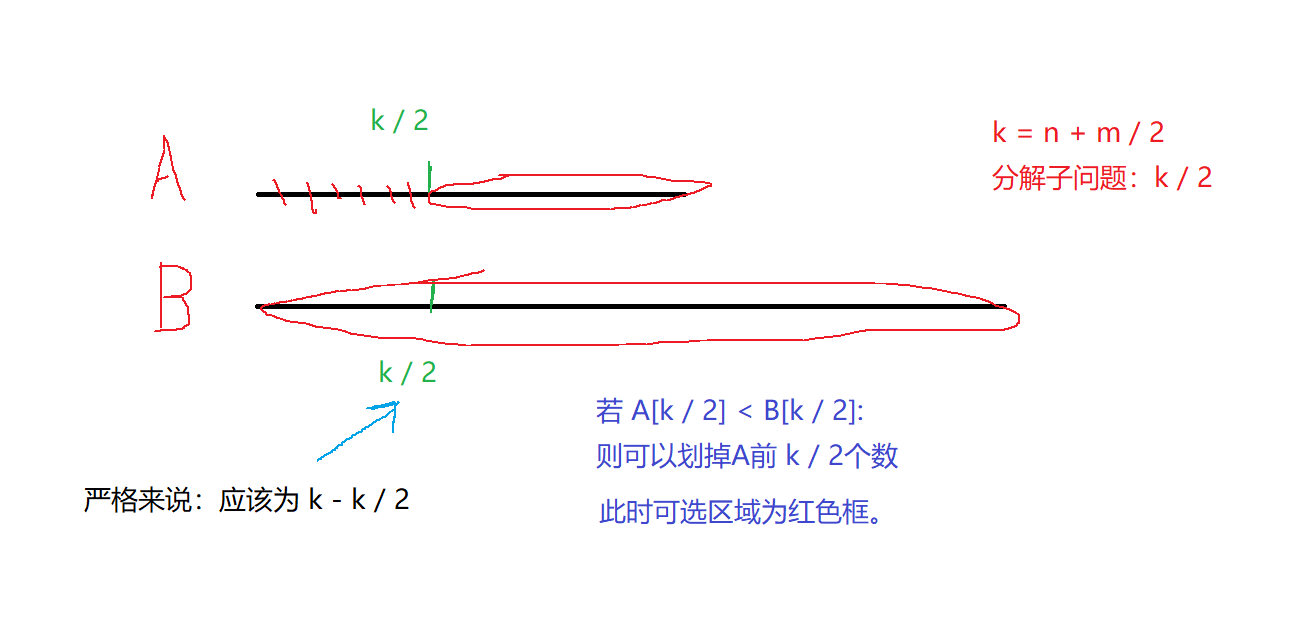
先进行判断：保证函数参数 nums1为较短的数组，nums2为较长的数组。

1、假设 m, n >= k/ 2，即 k / 2 的位置不会越界。

这样会有三种情况：

虽然从两个数组各选了k / 2 个值，但是第k小不一定在这k个数内。

但是却可以确定，第k小的数一定不在较小的数组那 k /2 的范围，这时可以舍弃 k / 2 的数据量，转而求舍弃后的两个数组（即被截取前 k / 2个数的数组和完整的另一个数组）

若两个值相等就简单了：两个 k / 2 的序列合起来就是两个数组的前 k 小的序列，即第k 小为任意一个 nums1[k / 2 - 1]或 num2[k / 2 - 1]

注意：相等情况的特殊之处：并不能直接返回，因为可能执行到某个阶段，不一定某个序列还有 k / 2个数。所以这个边界情况会导致当前数就不是第 k 小数了！

所以：最终只分两种情况即可： < 和 >

注意：k从1开始，下标从0开始！

  • nums1[k / 2 - 1] < nums2[k / 2 - 1]：
  • nums1[k / 2 - 1] > nums2[k / 2 - 1]：
  • nums1[k / 2 - 1] = nums2[k / 2 - 1]：

2、若 m < k / 2，则 nums1[k / 2]会发生越界

m 对应较短数组的长度，发生越界则将其规约到他的最大长度：si = min((int)nums1.size(), i + k / 2)

3、具体情形

  • find()：i， j 为起始位置
  • 递归出口：
    • k == 1：nums1为空，则return nums2[j]，否则return min(nums1[i], nums2[j])
    • k != 1：nums1为空，则return nums2[j + k -1]（j为nums2的起始下标，k从1开始）
  • si规约：si = min((int)nums1.size(), i + k / 2)
  • < >：
    • nums1[si - 1] > nums2[sj - 1]：则return find(nums1, i, nums2, sj, k - (sj - j));
    • nums1[si - 1] <= nums2[sj - 1]：（关于等于处理请看上面红字），则return find(nums1, si, nums2, j, k - (si - i));

注意：si - i 和 sj - j 为砍掉的数目！

关于 k / 2 和 k - k / 2：由于奇偶问题，k / 2，不一定和 k - k / 2相等！

注意：vector.size()返回值为size_type，需要使用 int强转一下。

==时间复杂度：O(log(m + n))==

AC代码2：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        if(len & 1){
            return find(nums1, 0, nums2, 0, (len >> 1) + 1);
        }else{
            int left = find(nums1, 0, nums2, 0, len >> 1);
            int right = find(nums1, 0, nums2, 0, (len >> 1) + 1);
            return (left + right) / 2.0;
        }
    }

    int find(vector<int>& nums1, int i, vector<int> nums2, int j, int k){
        // 始终保证较小的传给参数nums1
        if(nums1.size() - i > nums2.size() - j) return find(nums2, j, nums1, i, k);
        if(k == 1){
            // nums1为空
            if(nums1.size() == i) return nums2[j];
            return min(nums1[i], nums2[j]);
        }
        // nums1为空
        if(nums1.size() == i) return nums2[j + k -1];
        // si 规约       k / 2 和 k - k / 2
        int si = min((int)nums1.size(), i + k / 2), sj = j + k - k / 2;
        // （规约）后的两种情况
        if(nums1[si - 1] > nums2[sj - 1]) 
            return find(nums1, i, nums2, sj, k - (sj - j));   
        else
            return find(nums1, si, nums2, j, k - (si - i));
    }
};