题目链接：32.最长有效括号

题解：

又是动态规划的题，需要多加理解与按步骤走；同时使用栈也可以巧妙的解决！

题目简述：

给定一个包含左右括号的字符串，需要求出最长的有效匹配括号的子串的长度！

题解一：使用栈

首先，先回忆一下括号匹配的两个条件？

上次的括号问题有提到的，点击这里！

  1. 左右括号相等
  2. 任意前缀左括号数量大于等于右括号数量

接下来，我们可以将该括号序列分为若干段：

  • 从前向后找，找到右括号大于左括号的位置，此时就是一段合法区间
  • 从所有合法区间中找到一个最大匹配有效长度即可

参考下面的图：

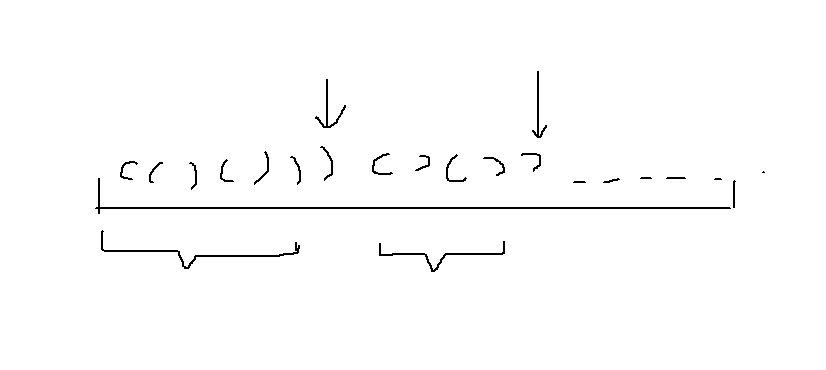
具体操作：

使用start标记可匹配区间的上一个元素，即每次出现的右大于左的位置！

  1. 遇到左括号直接进栈
  2. 遇到右括号：
    1. 若栈不空，说明没走到右大于左的位置，此时栈顶元素与之对应的左括号出栈
      1. 如果出栈后栈空，说明从起点start到当前位置i是一组有效括号序列，更新最大值
      2. 如果出栈后不空，说明栈顶到当前位置i是一组有效括号序列，更新最大值
    2. 若栈为空，说明已经走到右大于左的位置，此时更新start为当前位置i

AC代码一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> stk;
        int res = 0;
        for(int i = 0, start = -1; i < s.size(); i++){
            if(s[i] == '(') stk.push(i);
            else{
                if(stk.size()){
                    stk.pop();
                    if(stk.size()) res = max(res, i - stk.top());
                    else res = max(res, i - start);
                }else start = i;
            }
        }
        return res;
    }
};

题解二：动态规划

参考题解：点击这里！

题目中提到了最长，可以考虑使用动态规划解题！

同样分为两步：

  1. 状态表示：一个字符串，使用一维数组dp[i]，表示以s[i]为结尾的字符串中有效括号的最大长度（包括i）
  2. 状态计算：
    1. 若s[i]为左括号，由于左括号不可能和之前括号组合为有效括号，故 dp[i] = 0
    2. 若s[i]为右括号：
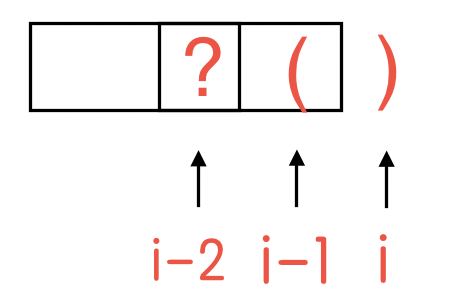
      1. 若s[i - 1]为左括号，形如：...()，此时dp[i] = 2；若相邻的之前还有匹配括号，则dp[i] += dp[i - 2]，见下方图一！
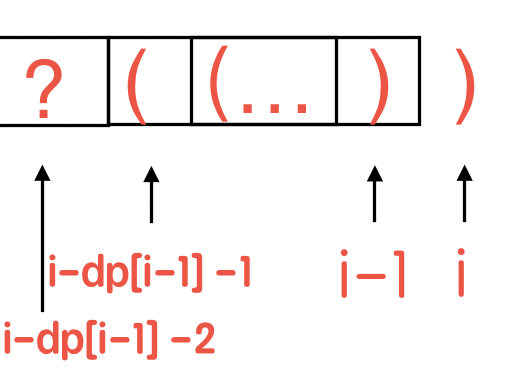
      2. 若s[i - 1]为右括号，形如：...))，则此时只有保证当前右括号有匹配项，即dp[i - 1] > 0，形如：...(...))；并且保证s[i]也有括号匹配，即s[i - dp[i - 1] - 1] == '('，形如：...((...))，这样才可完成s[i]的匹配，此时dp[i] = dp[i - 1] + 2；若与s[i]匹配的左括号相邻的之前还有匹配括号，形如：.(..)((...))，则dp[i] += dp[i -dp[i - 1] - 2]，见下方图二！

图一：

图一

图二：

图二

AC代码二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int longestValidParentheses(string s) {
        vector<int> dp(s.size());
        int res = 0;
        for(int i = 1; i < s.size(); i++){
            if(s[i] == ')'){
                if(s[i - 1] == '('){
                    dp[i] = 2;
                    if(i - 2 >= 0) dp[i] += dp[i - 2];
                }else if(dp[i - 1] > 0 && i - dp[i - 1] - 1 >= 0 && s[i - dp[i - 1] - 1] == '('){
                    dp[i] = dp[i - 1] + 2;
                    if(i - dp[i - 1] - 2 >= 0) dp[i] += dp[i -dp[i - 1] - 2];
                }
                res = res < dp[i] ? dp[i] : res;
            }
        }
        return res;
    }
};