题目链接：11.盛最多水的容器

题解：

双指针使用，巧妙的思路！

也是不太好理解！多看看！

题目简述：

给了一堆柱子及其高度，要求选出两个柱子，使得凹槽内的面积达到最大，当然两根柱子要选较低的一根作为高，否则会发生漏水！

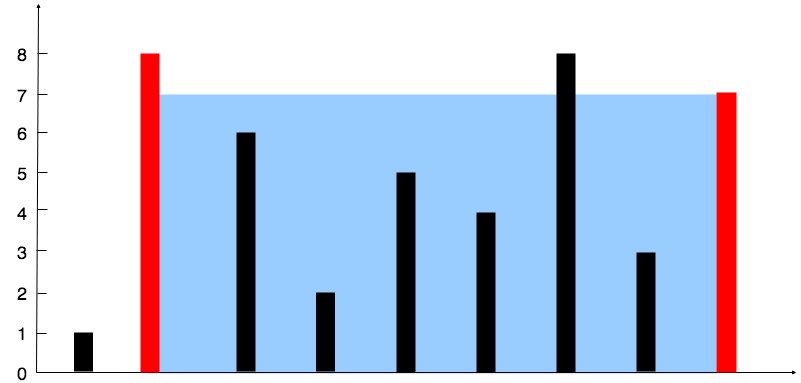
题解一：

本题可以使用暴力，直接两层循环，但是会超时！

所以可以使用双指针算法：

先给出具体思路：两个指针（i 和 j）一个从左走，一个从右走，若左边的比右边的高，则高的一边往内靠，即左面的往后走，右面的往前走，i++，j--，直到i == j结束。

给出证明一：

假设最优解对应的下标为i', j'（i' < j'），在两指针（i, j）移动的过程中不断靠近最优解，先假设i 先走到 i'，且此时j' < j。

反证：假设此时 a[i] <= a[j]，用s表示i,j盛水的面积，s'表示i',j'盛水的面积，则：

  1. s = min(a[i], a[j]) * (j - i) = a[i] * (j - i)
  2. s' = min(a[i'], a[j']) * (j' - i') = min(a[i], a[j']) * (j' - i) <= a[i] * (j' - i) < a[i] * (j - i) = s
  3. 即如果a[i] <= a[j]，则最优解 s'是小于 s的，发生矛盾！假设不成立。
  4. 结论：要想使i', j'为最优解，必须使a[i] > a[j]，这样可以使得j指针可以向前移动，逐渐靠近j'

可以结合我画的图来看：s‘面积最大为s2'

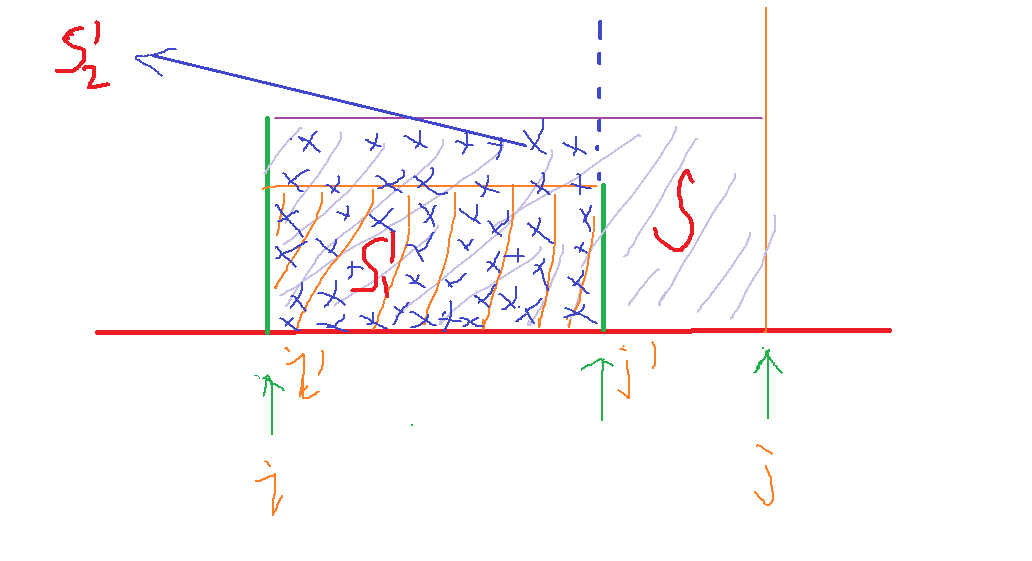
给出证明二：

题解来源：LeetCode

两个指分别指向两端，假设左边的较低！

如果固定左边的柱子，移动右边的柱子，那么水的高度一定不会增加，且宽度一定减少，所以水的面积一定减少。这个时候，左边的柱子和任意一个其他柱子的组合，其实都可以排除了（因为一定宽度变小，高度一定 <= 当前最小高度，面积一定减小）。也就是我们可以排除掉左边的柱子了。（即左边的柱子存在的毫无意义，固定左边右边移动一定不会使面积变大）

总结：较低的一方固定了，较高的一方进行移动，毫无意义，不会使得面积增大！所以要想得到最大值，一定是较长的一方固定，较短的一方移动。

时间复杂度：没根柱子只扫描一遍，为 O(N)

AC代码一：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxArea(vector<int>& height) {
        int res = 0;
        for(int i = 0, j = height.size() - 1; i < j;){
            res = max(res, min(height[i], height[j]) * (j - i));
            if(height[i] < height[j]) i++;
            else j--;
        }
        return res;
    }
};

题解二：

**这种好像更好理解！**同样是双指针！

  1. 想让i, j指向两边，此时的构成的矩形宽度是最大的，但是面积不一定是最大的，所以两个指针要想内游走。
  2. 对于此时i, j指向的直线，宽度是最大的，向内收敛的过程中，宽度是在减小的。如果遇到高度更低的柱子，那么现在构成的矩形面积一定会比原来的要小，毕竟宽度变小，高度变小；所以只有遇到高度更高的柱子，才有可能比当前的面积要大。
  3. 所以，遇到更短的直接向后走，遇到高的则做一下比较，留下最大值即可！

注意长短的比较是和上一次最短的比较！

时间复杂度：同样为 O(N)

其实代码意思一样的，换了个写法！

AC代码二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxArea(vector<int>& height) {
        int i = 0, j = height.size() - 1;
        int res = 0;
        while (i < j)
        {
            int h = min(height[i], height[j]);
            res = max(res, h * (j - i));
            while (i < j && height[i] <= h) i ++;
            while (i < j && height[j] <= h) j --;
        }
        return res;
    }
};